Programa

Tuesday, June 21, 2022

8:11 PM

 

<<Cronograma_CNiNo.pdf>>

 

 

Clases

domingo, 9 de marzo de 2025

00:57

 

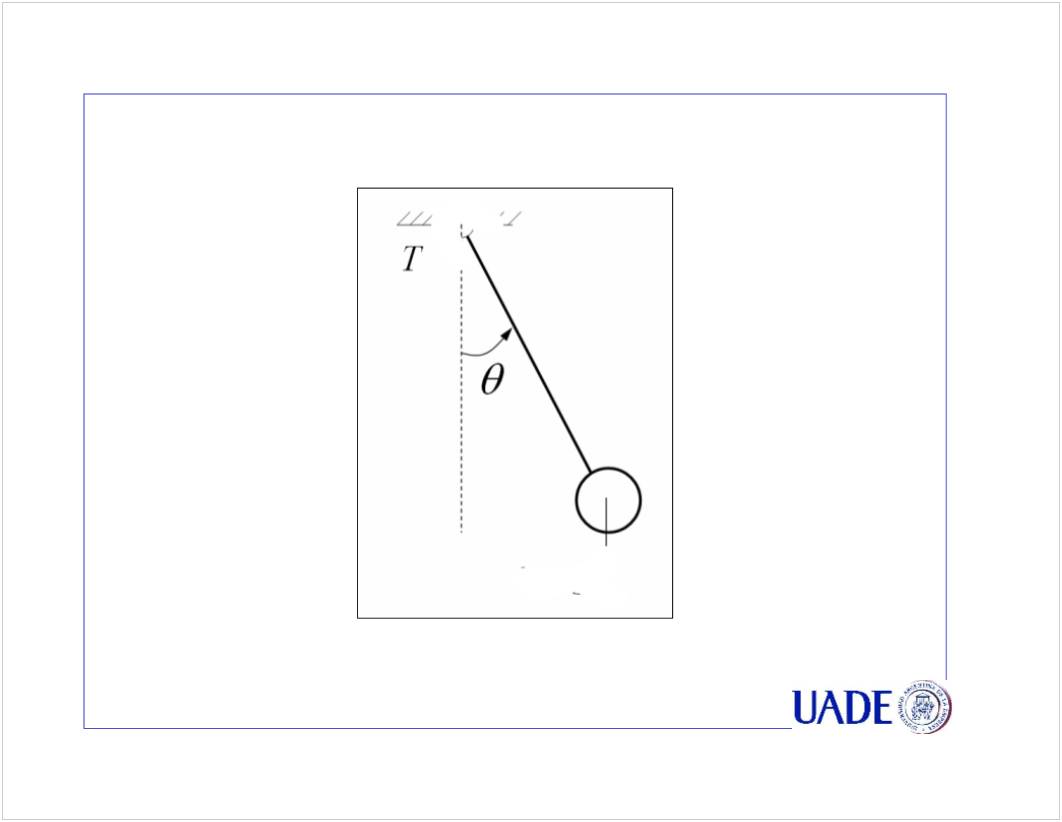
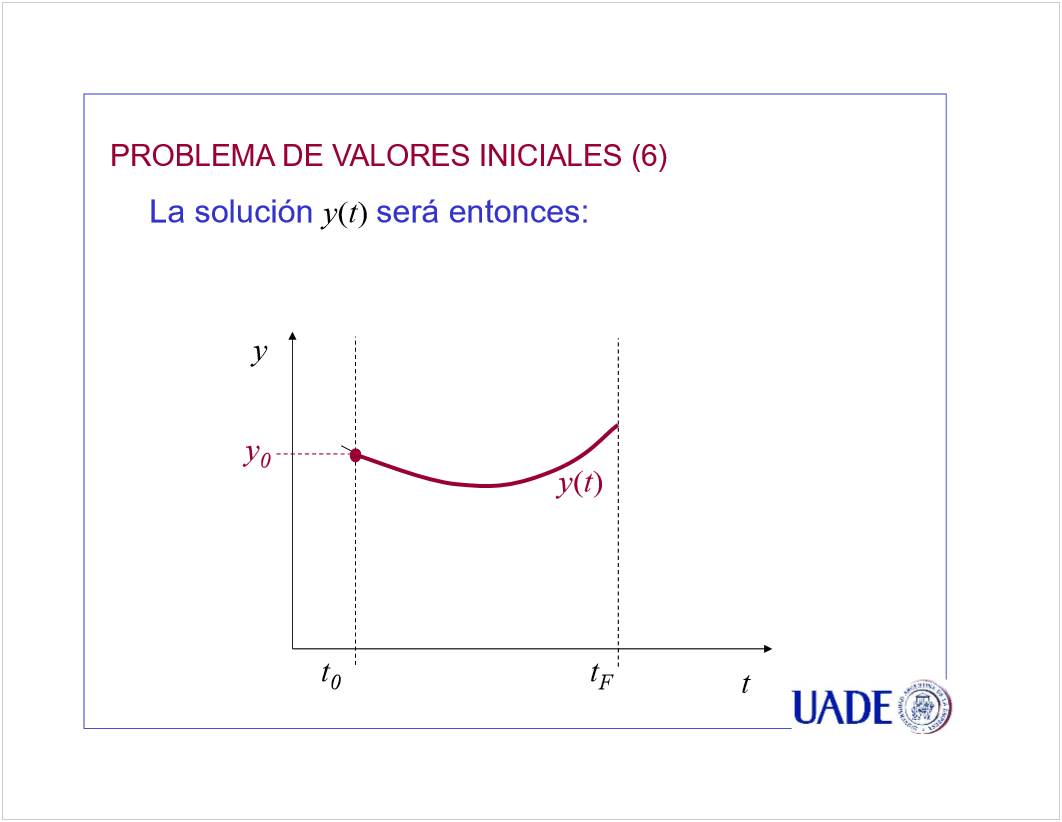
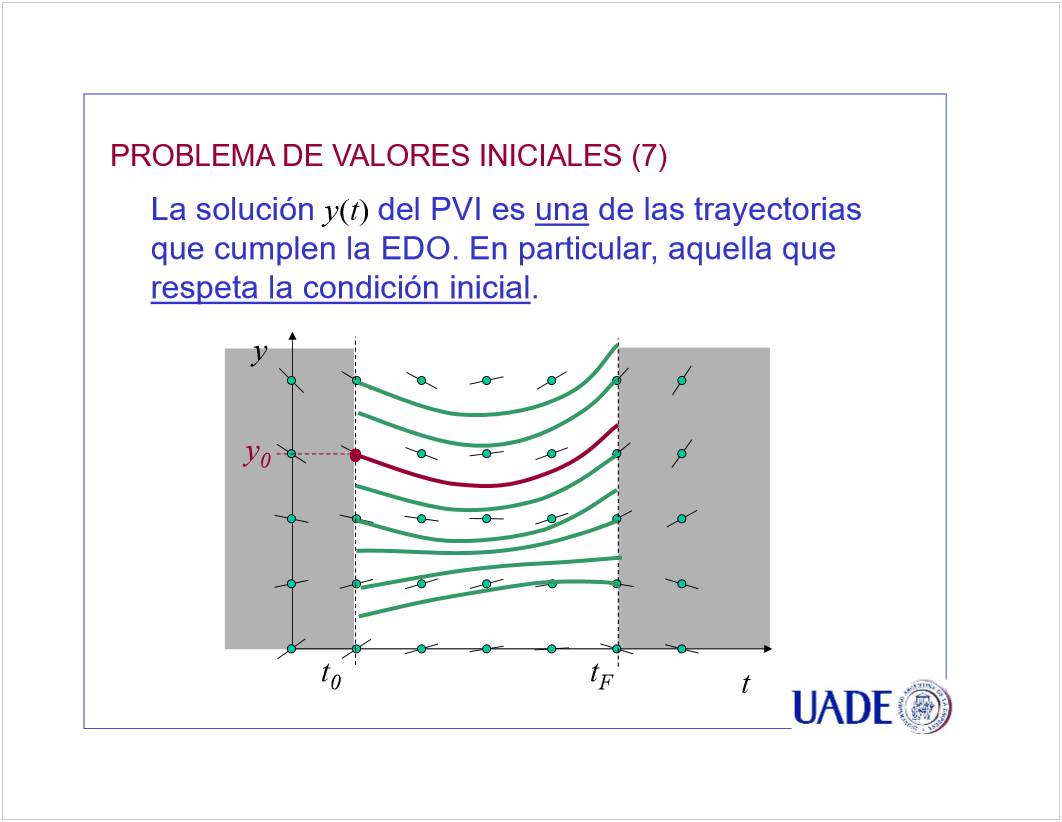
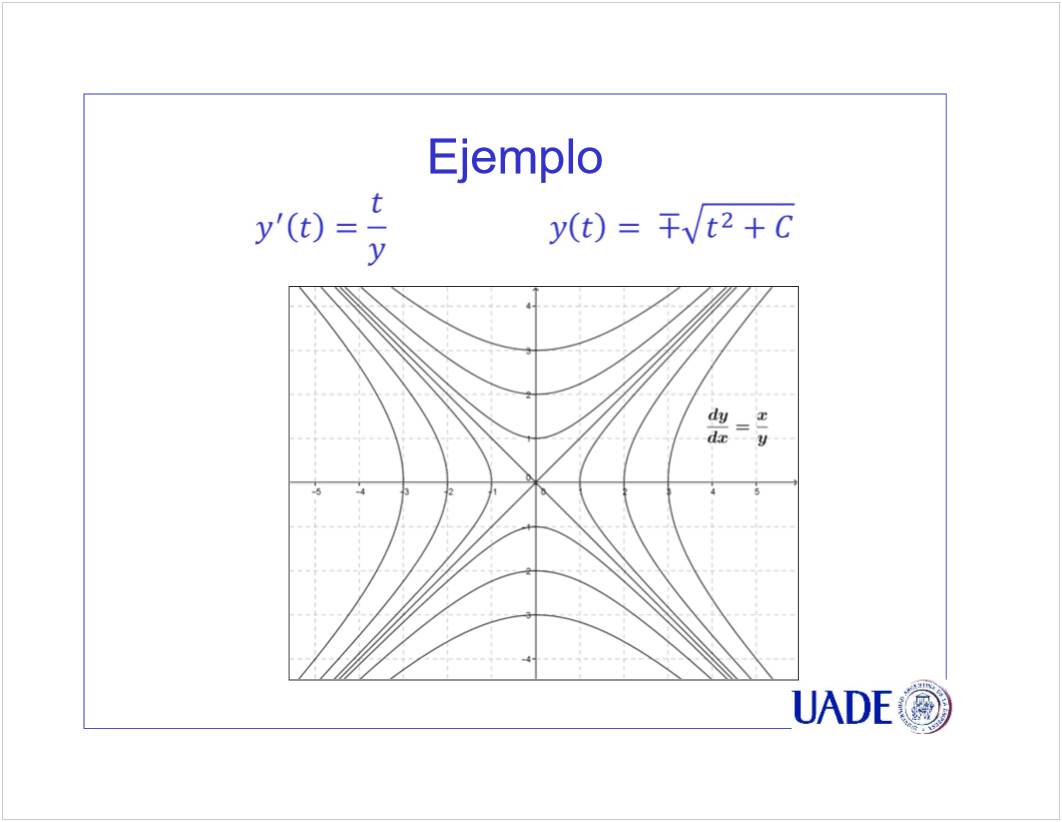
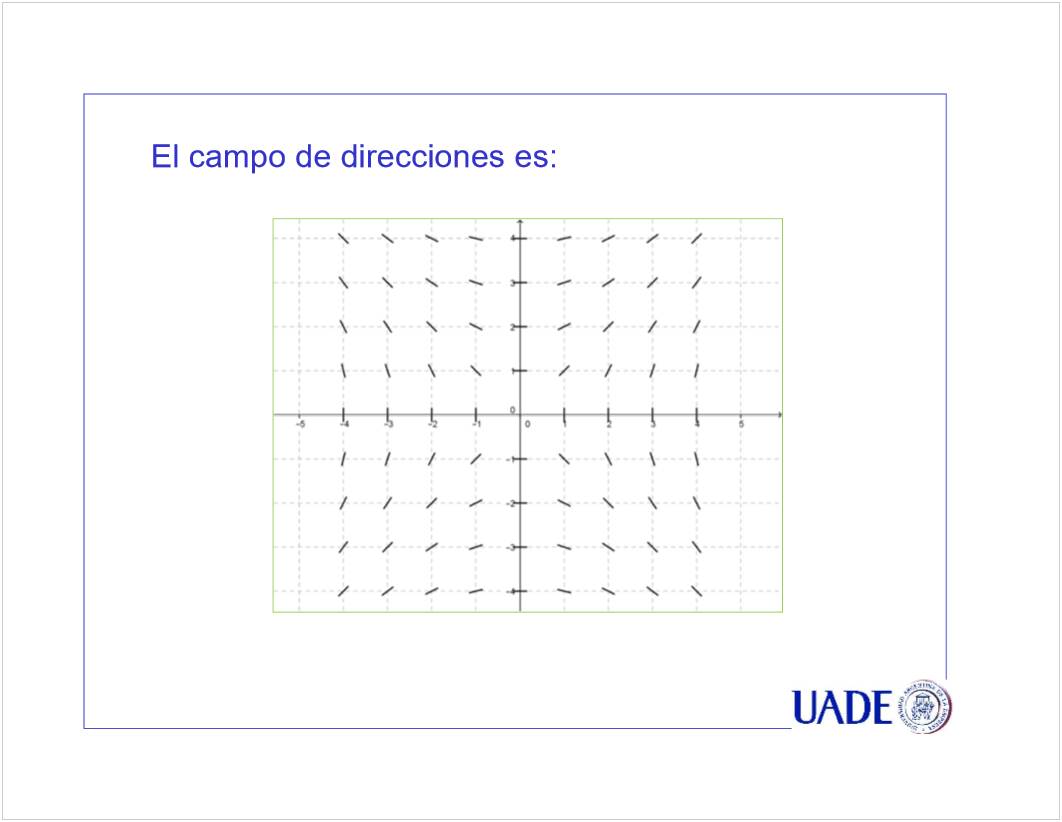
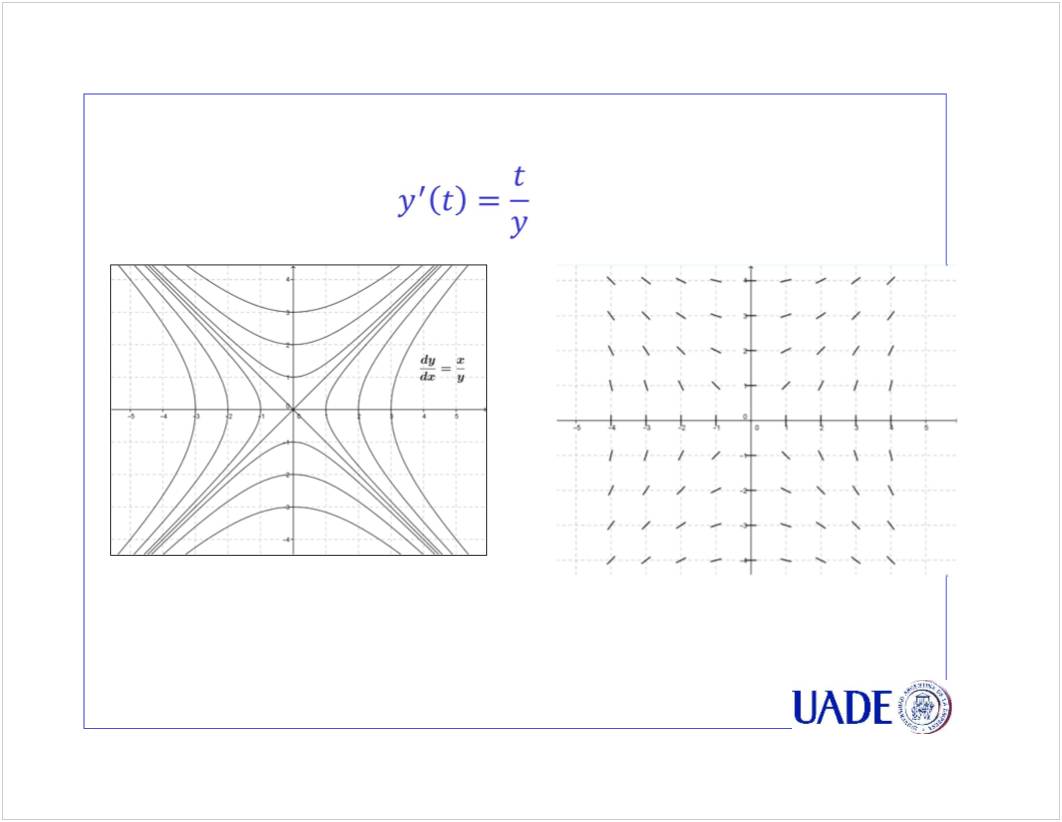
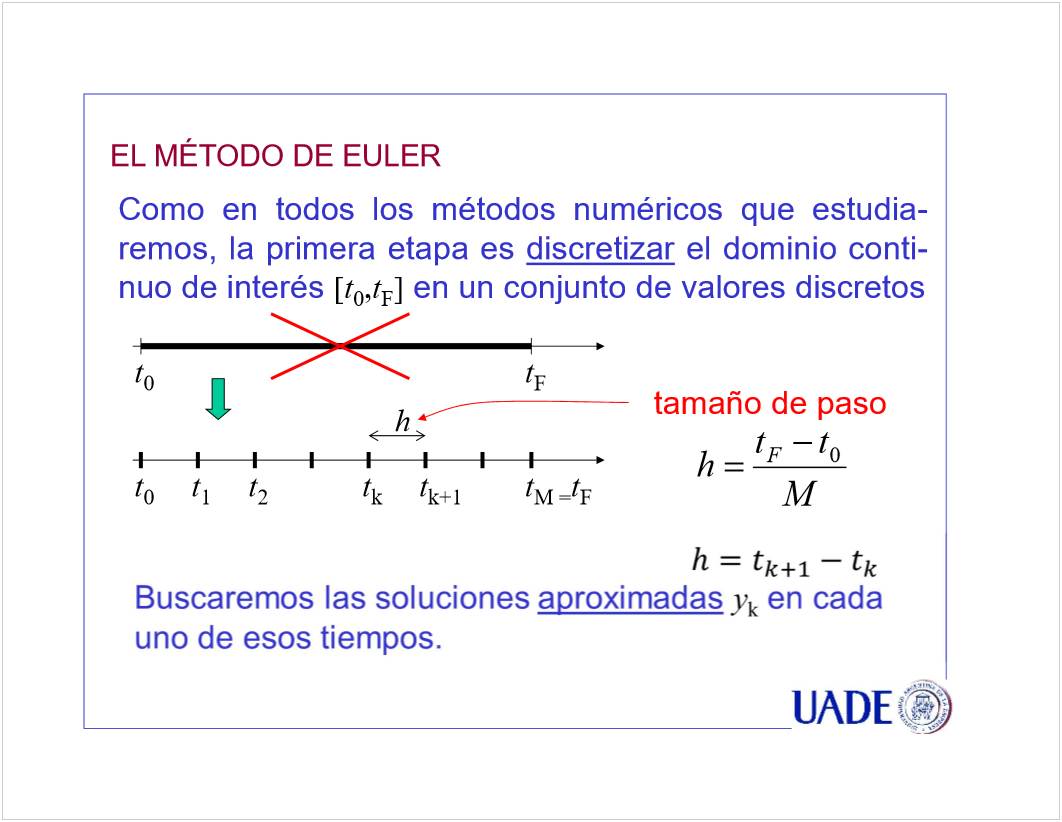
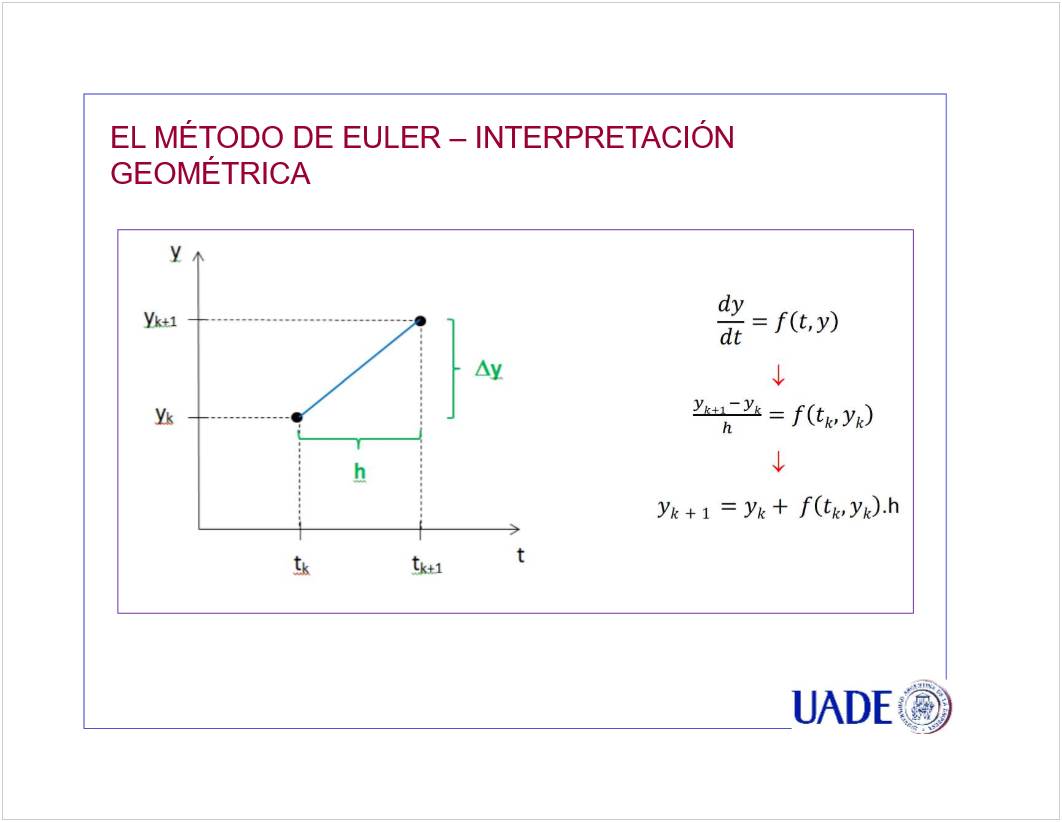
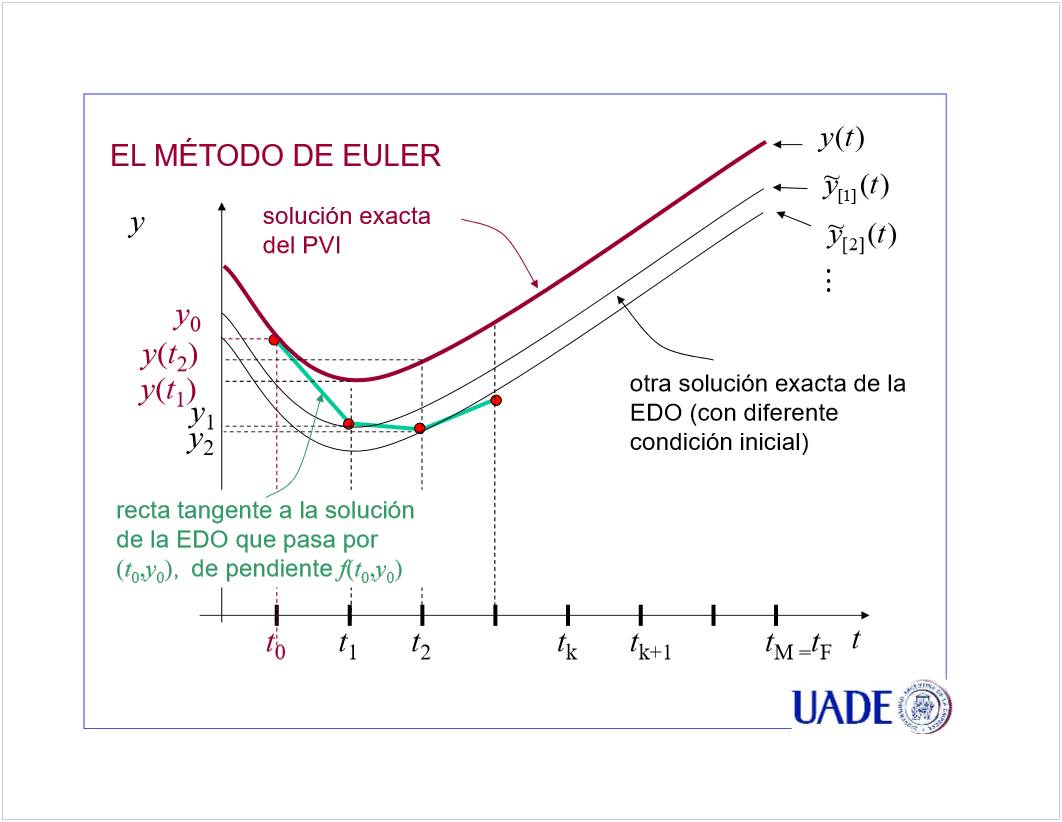
C1 - EDO 1er Orden

Wednesday, June 8, 2022

6:47 PM

 

 

 

 

<<CN01a EDO de 1er Orden - PVI Euler - 2021.pptx>>

 

 

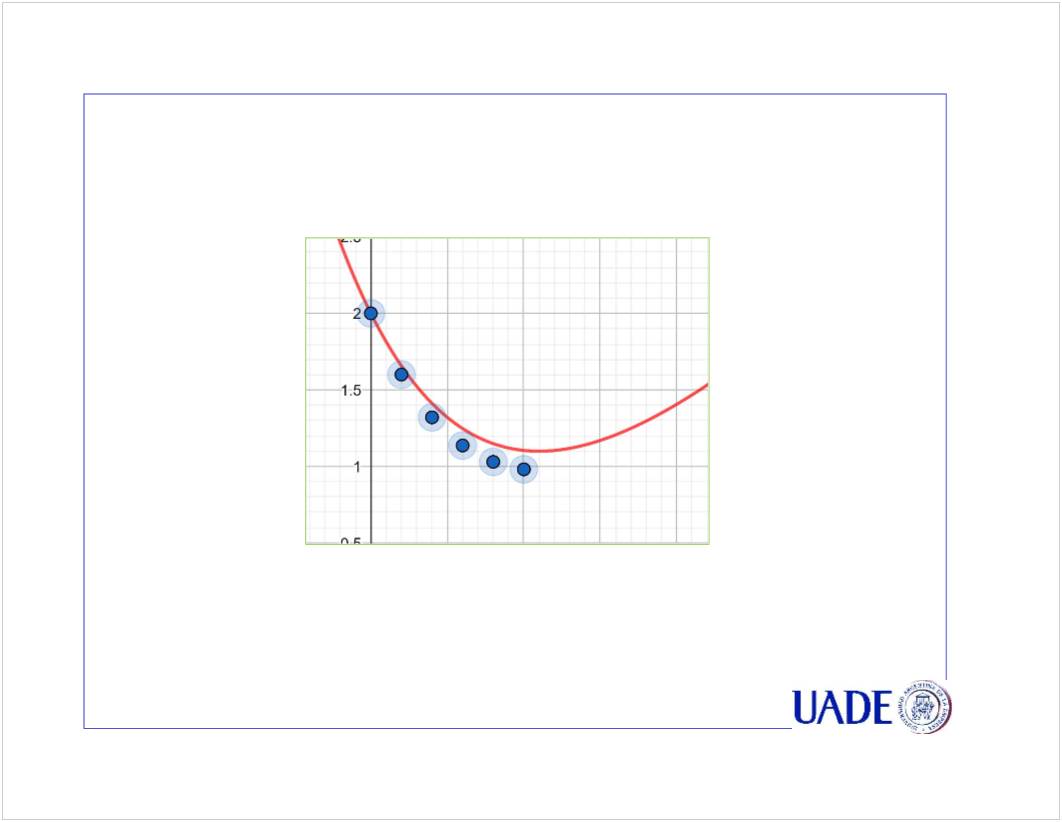
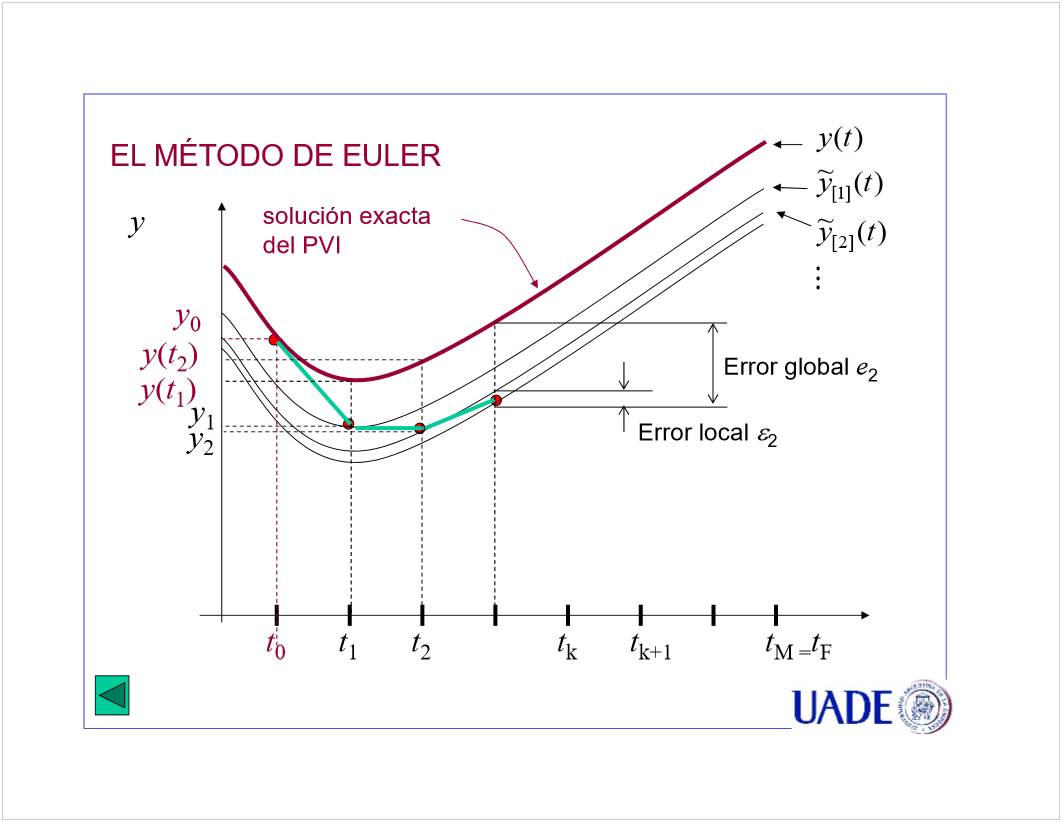
C1 - Runge Kutta Gi

Wednesday, June 8, 2022

6:48 PM

 

<<Runge Kutta Gi.ppt.pptx>>

 

 

 

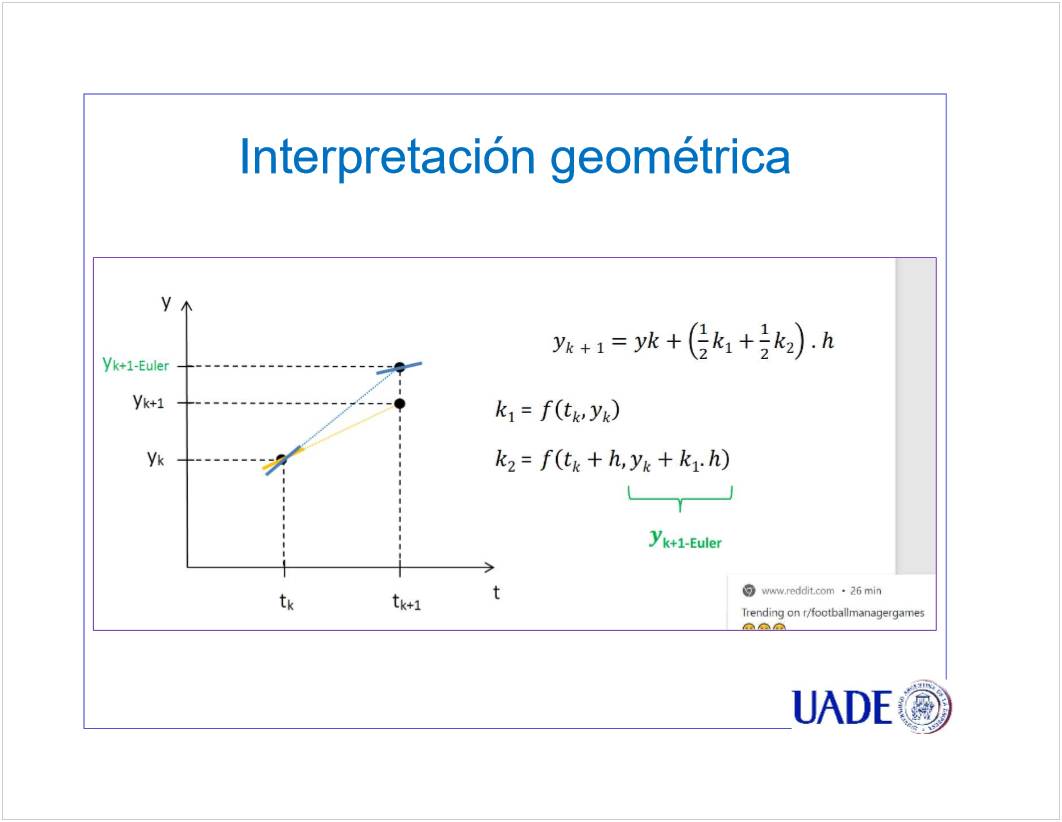
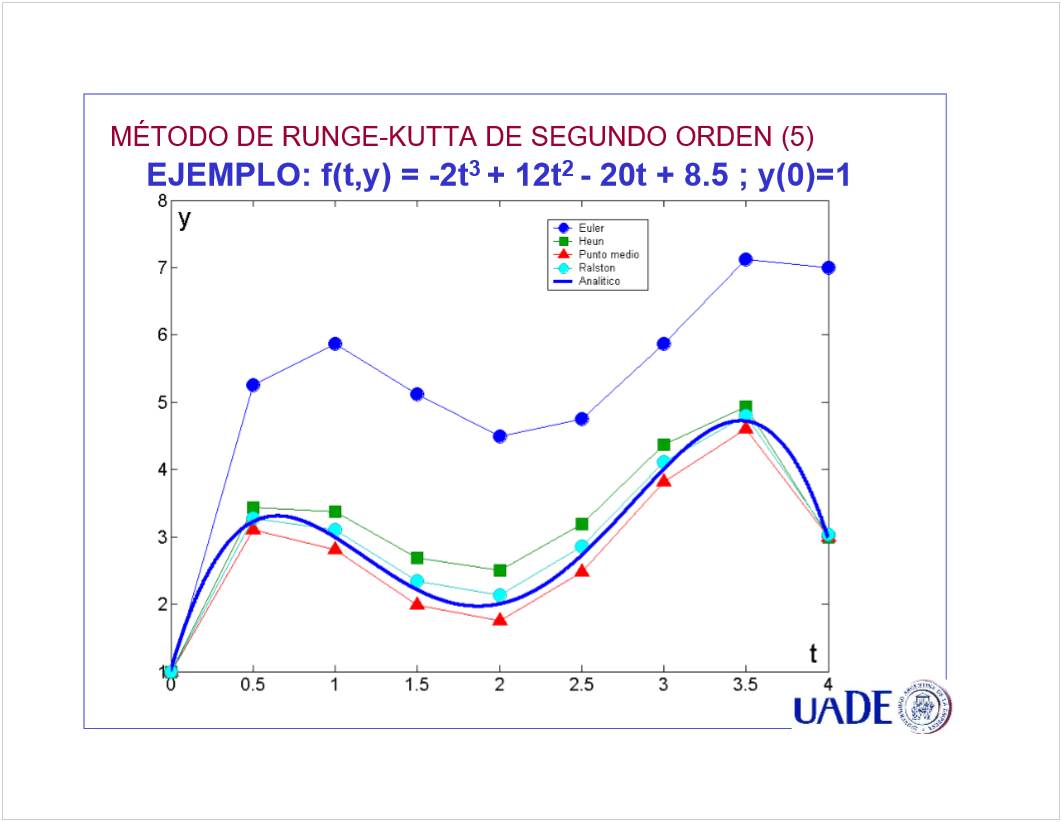
C2 - Sistemas EDO de 1er Orden

Wednesday, June 22, 2022

3:19 PM

 

<<CN02a EDO de 1er Orden - Sistemas  8_06.pptx>>

 

 

 

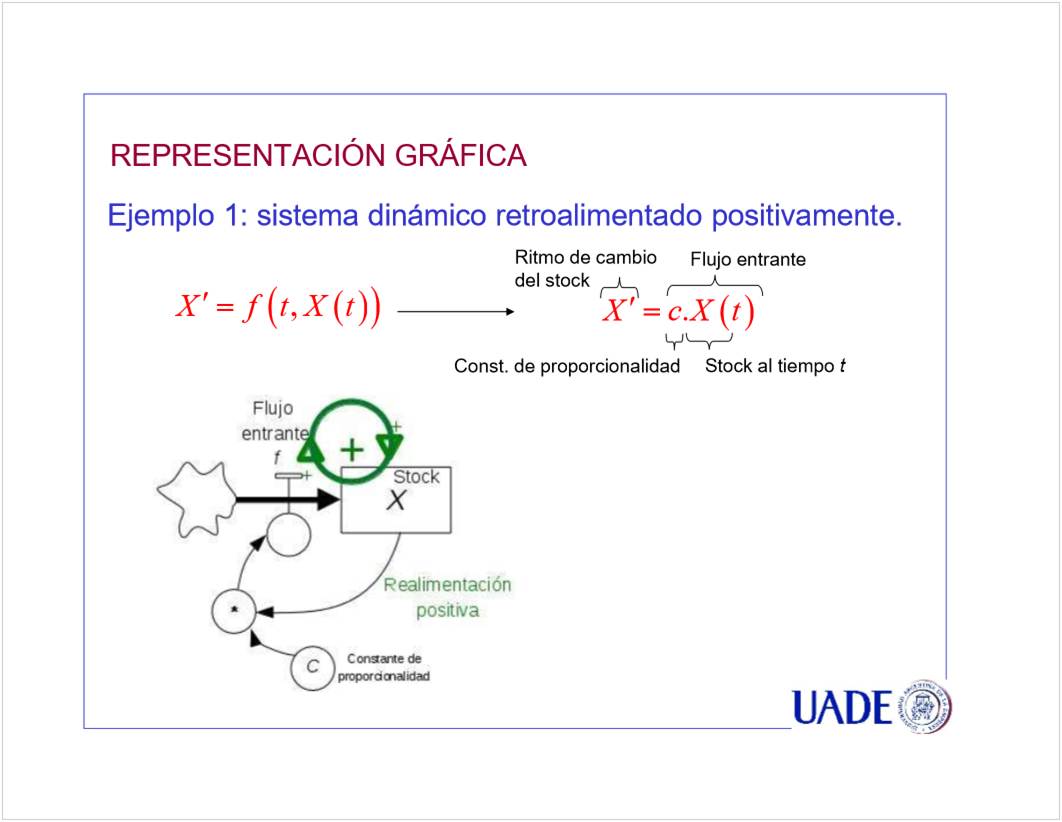
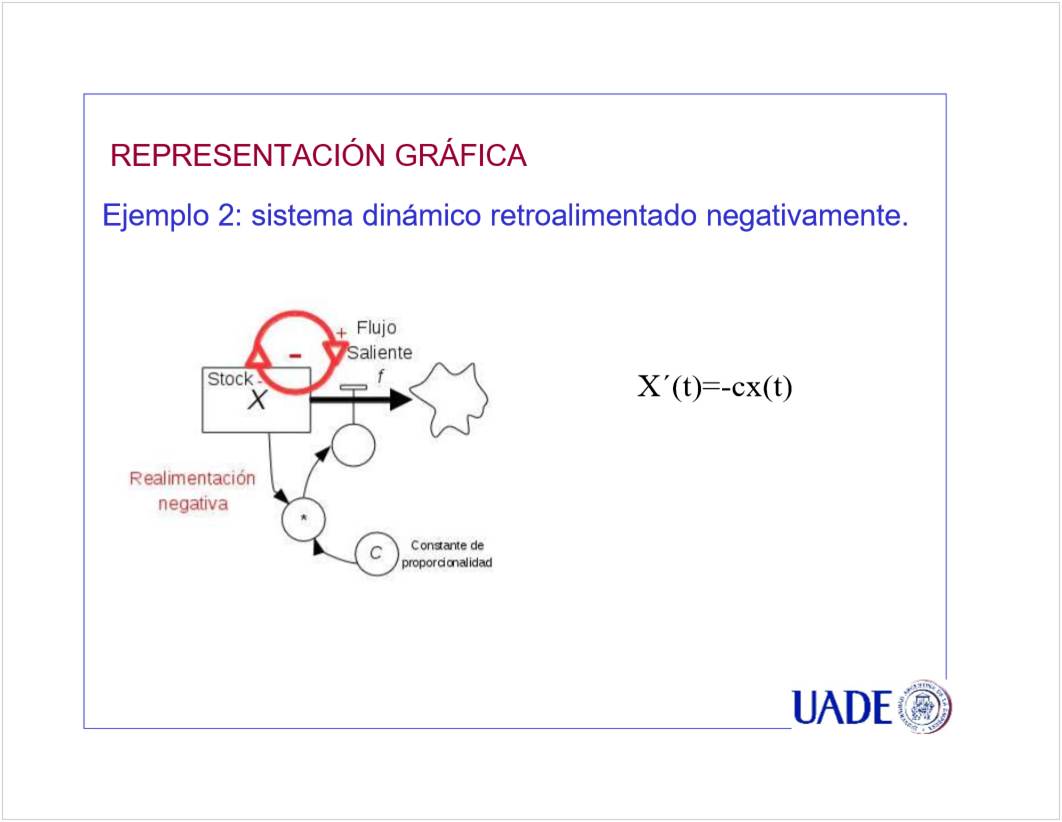
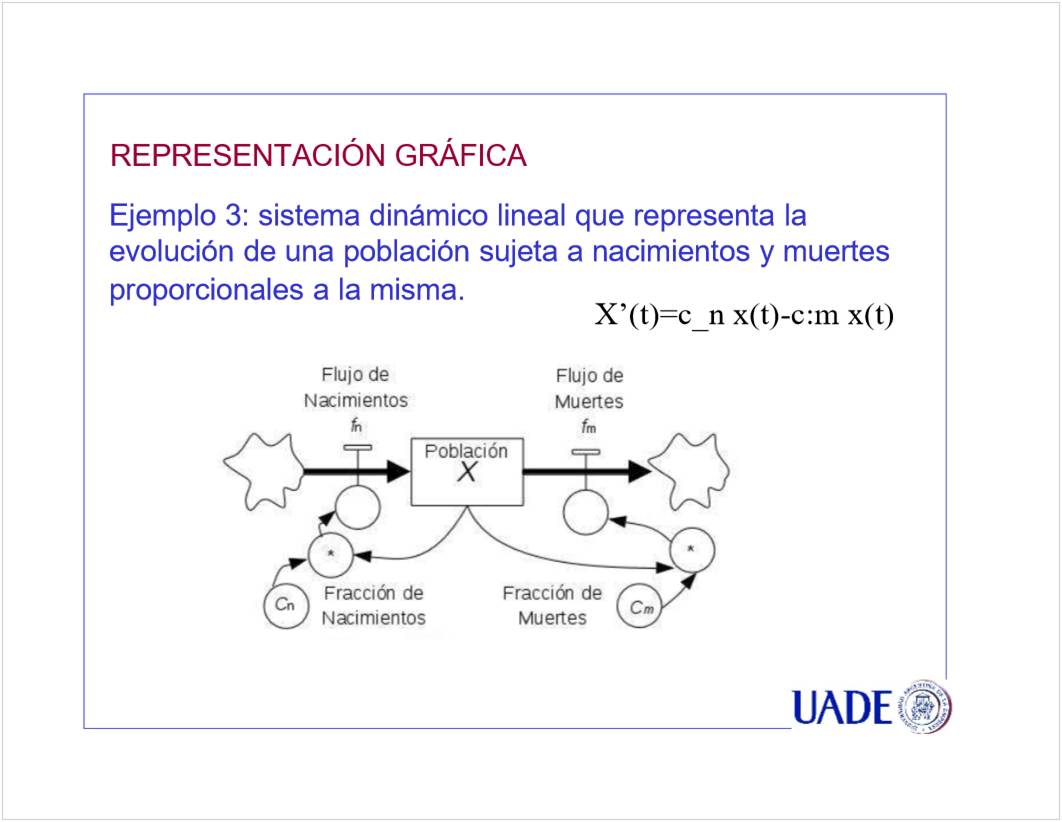
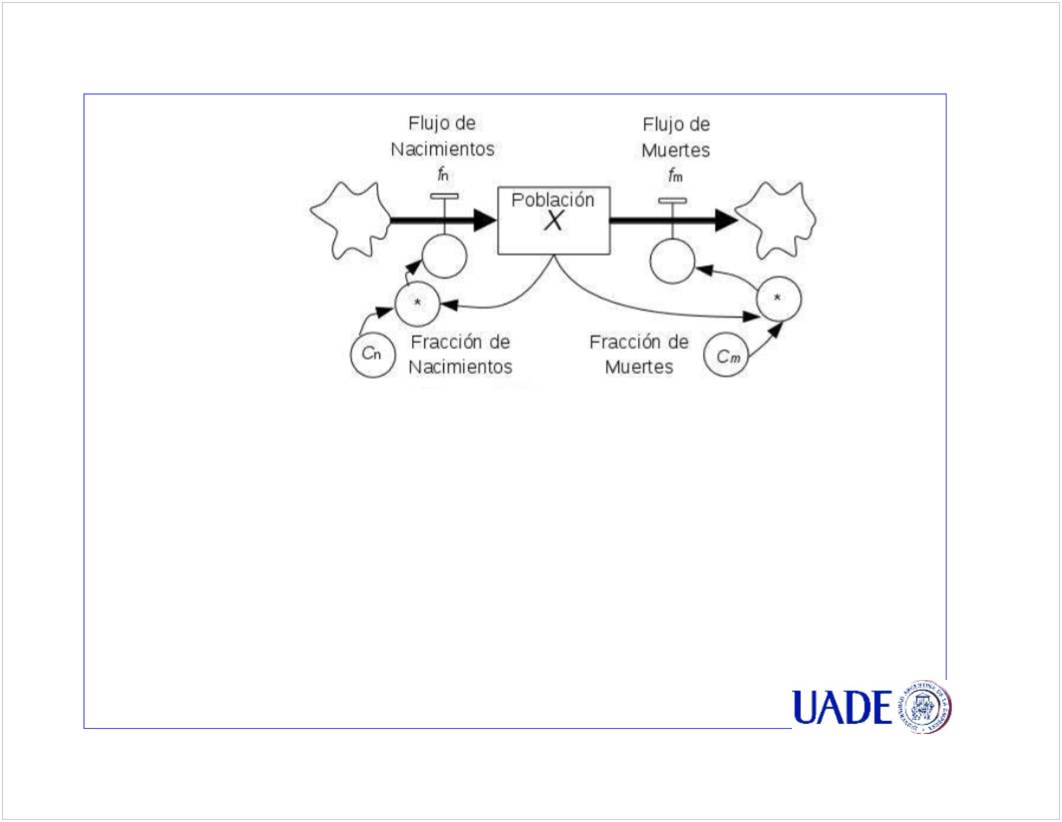
C2 - Stock y Flujo

Wednesday, June 22, 2022

3:20 PM

 

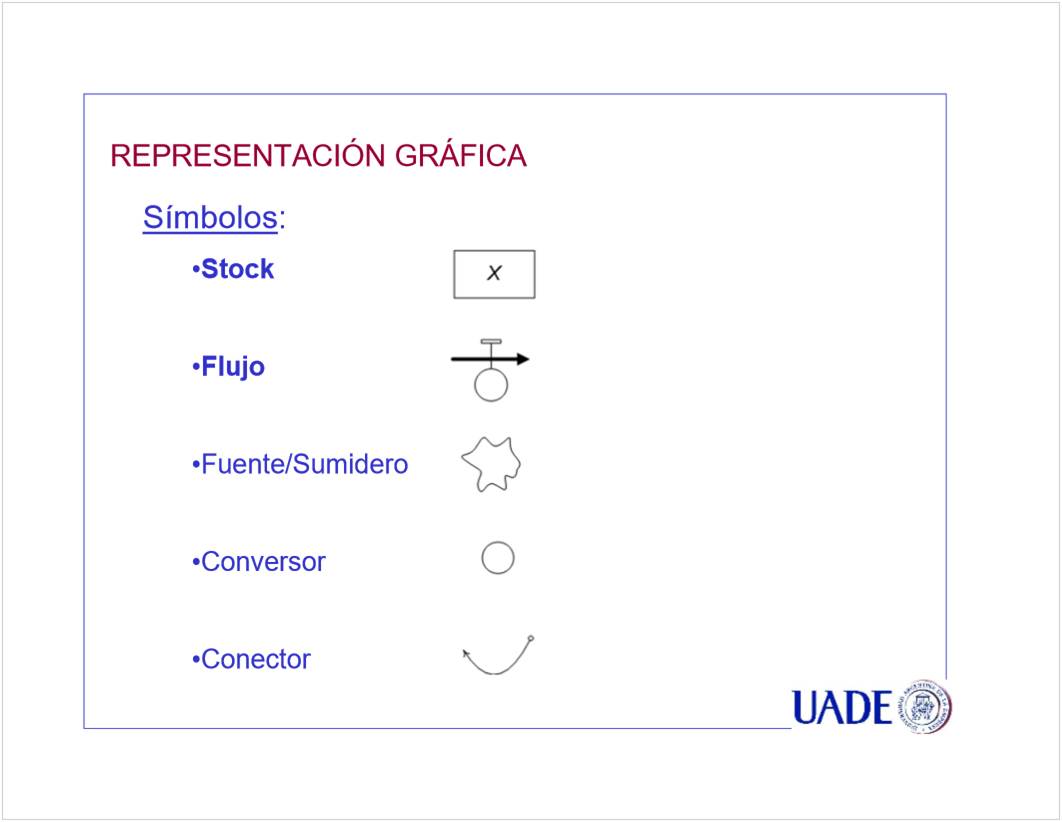
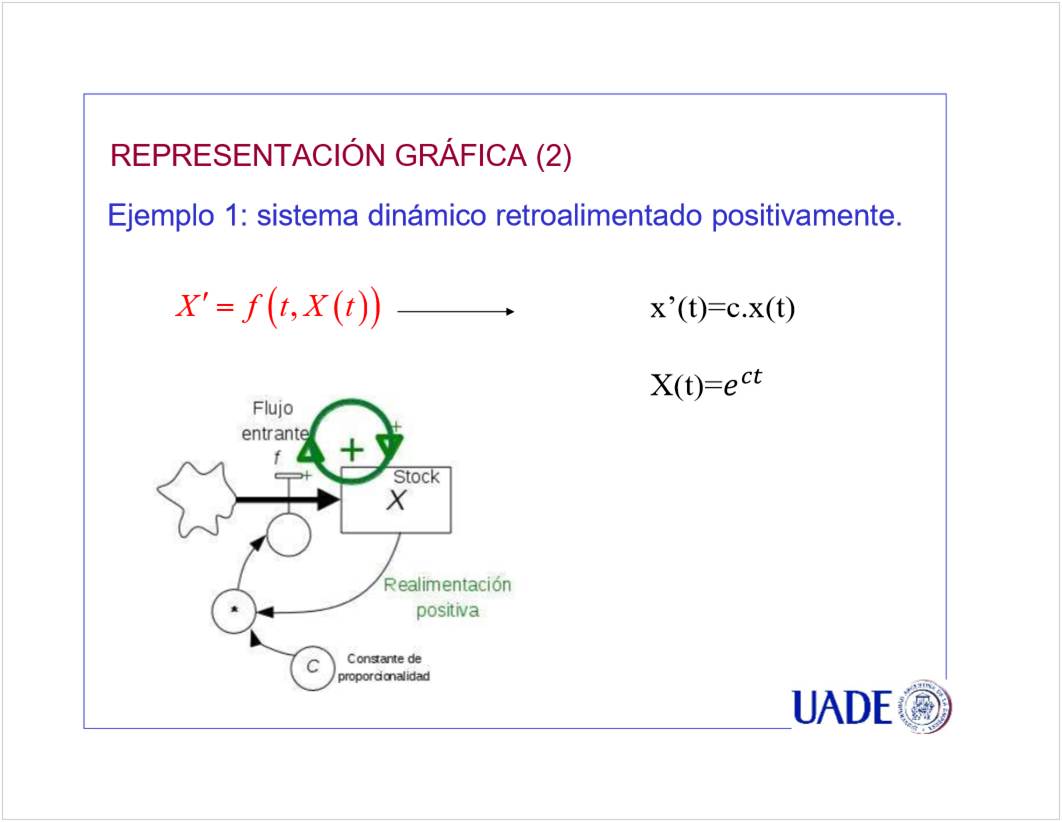
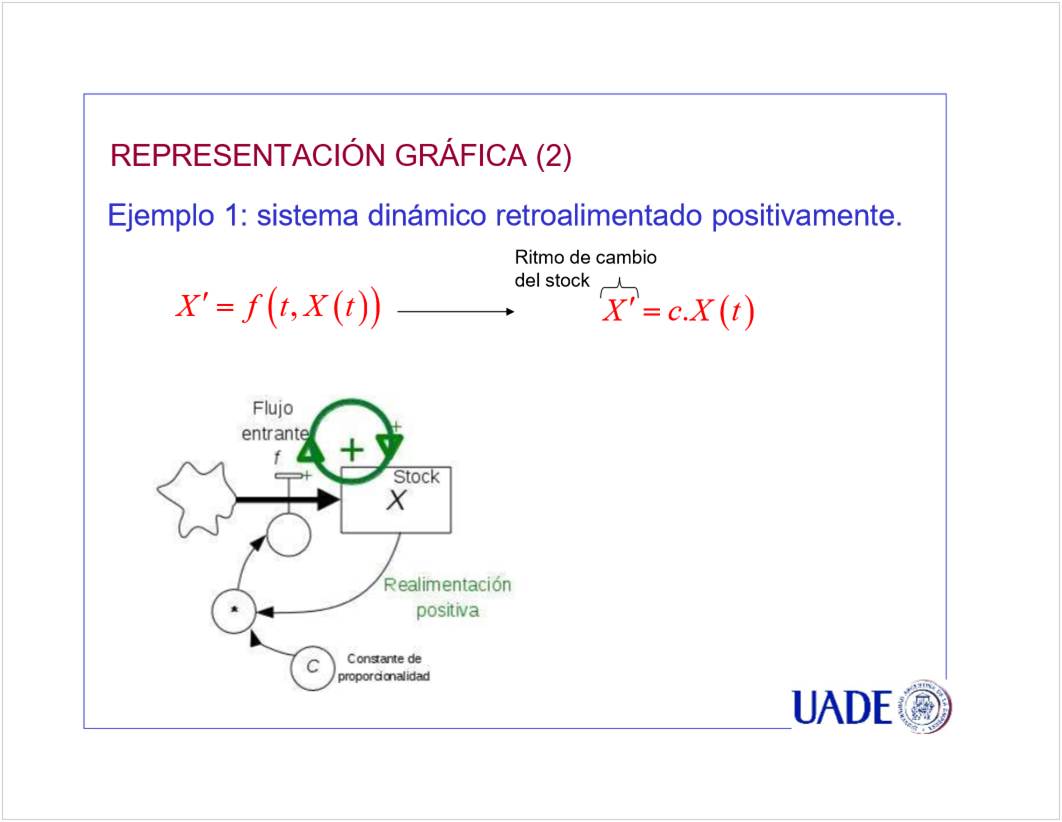
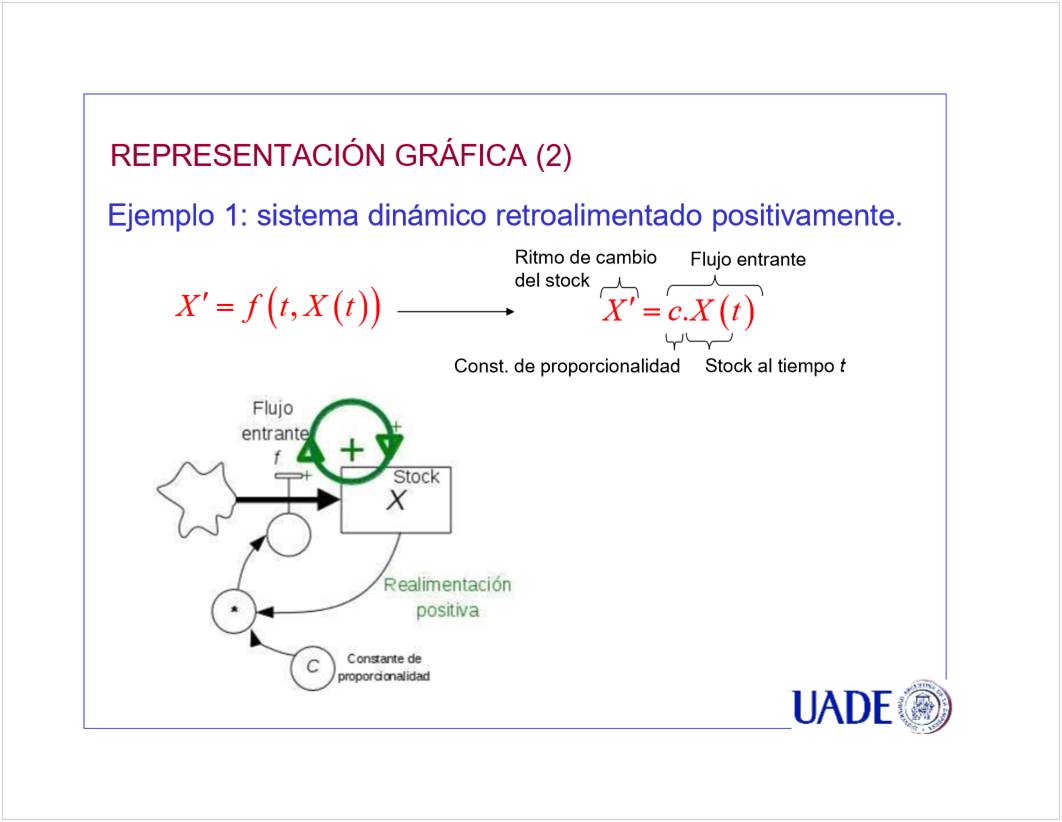
<<CN02b Stock y Flujo clase 08_6.pptx>>

 

 

 

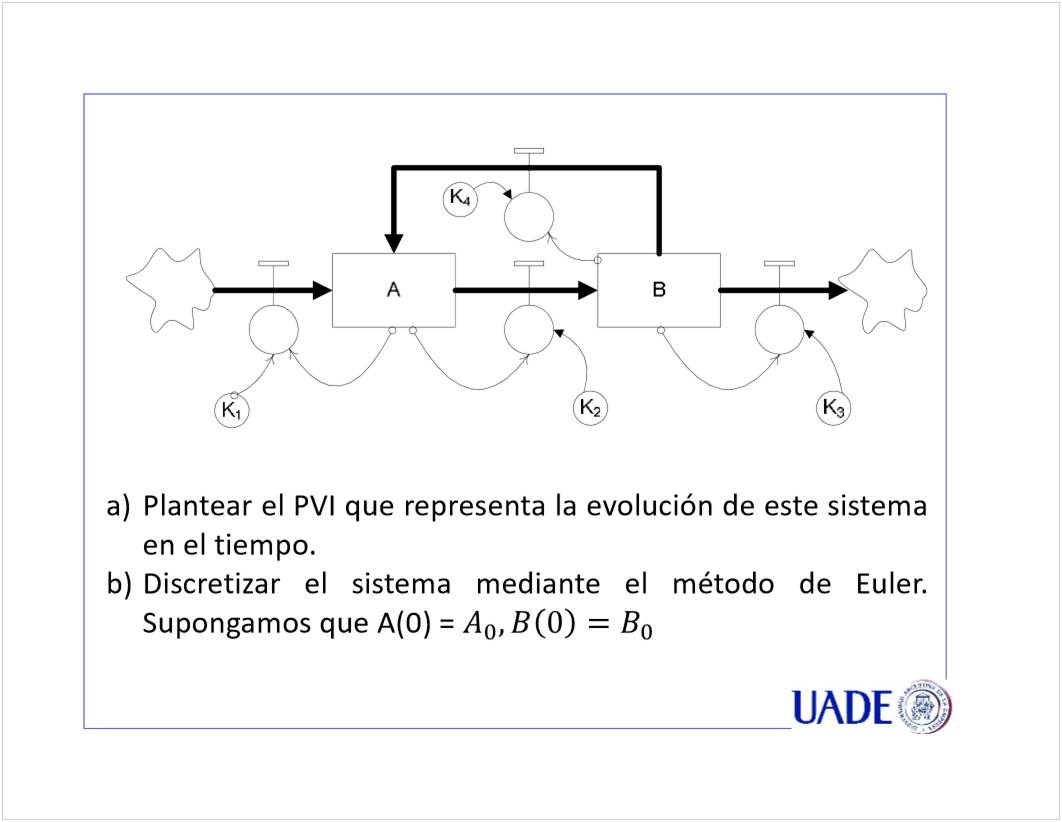
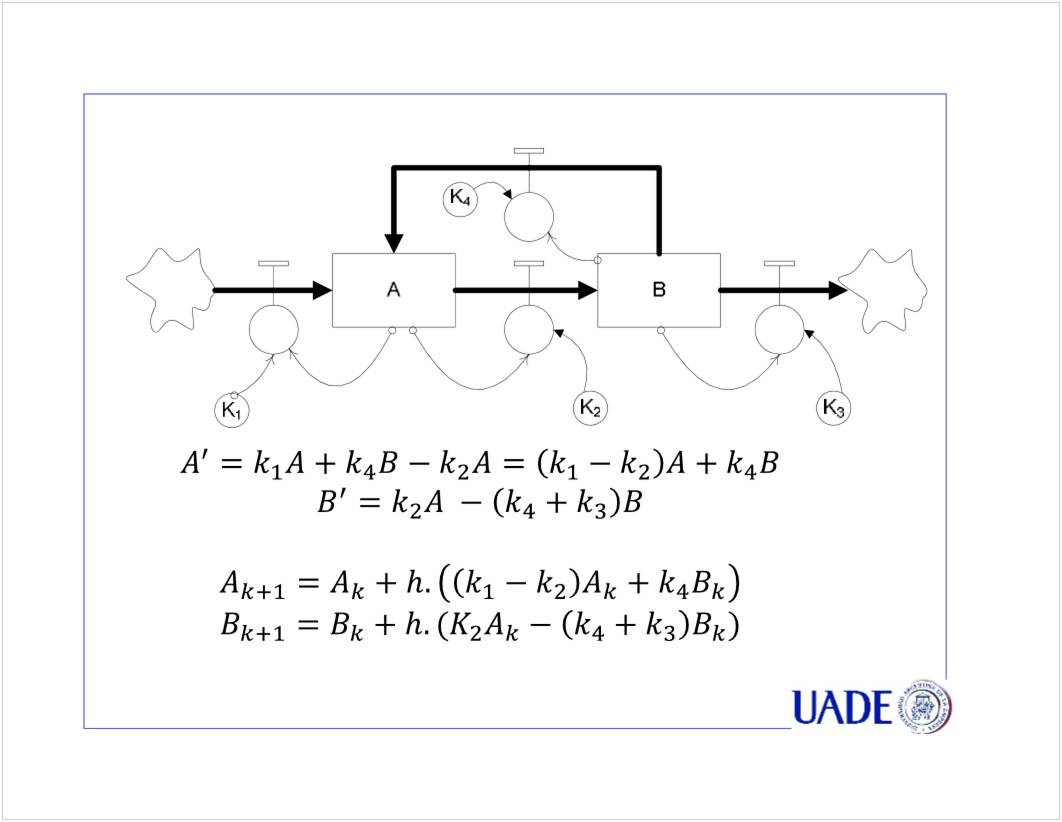
C3 - EDO Superior

Tuesday, June 21, 2022

8:16 PM

 

<<CN03 EDO de Orden Superior 15_6.ppt>>

 

C4 - EDO No lineales

Tuesday, June 21, 2022

8:22 PM

 

<<CN04 Ecuaciones No Lineales Gi.ppt>>

 

 

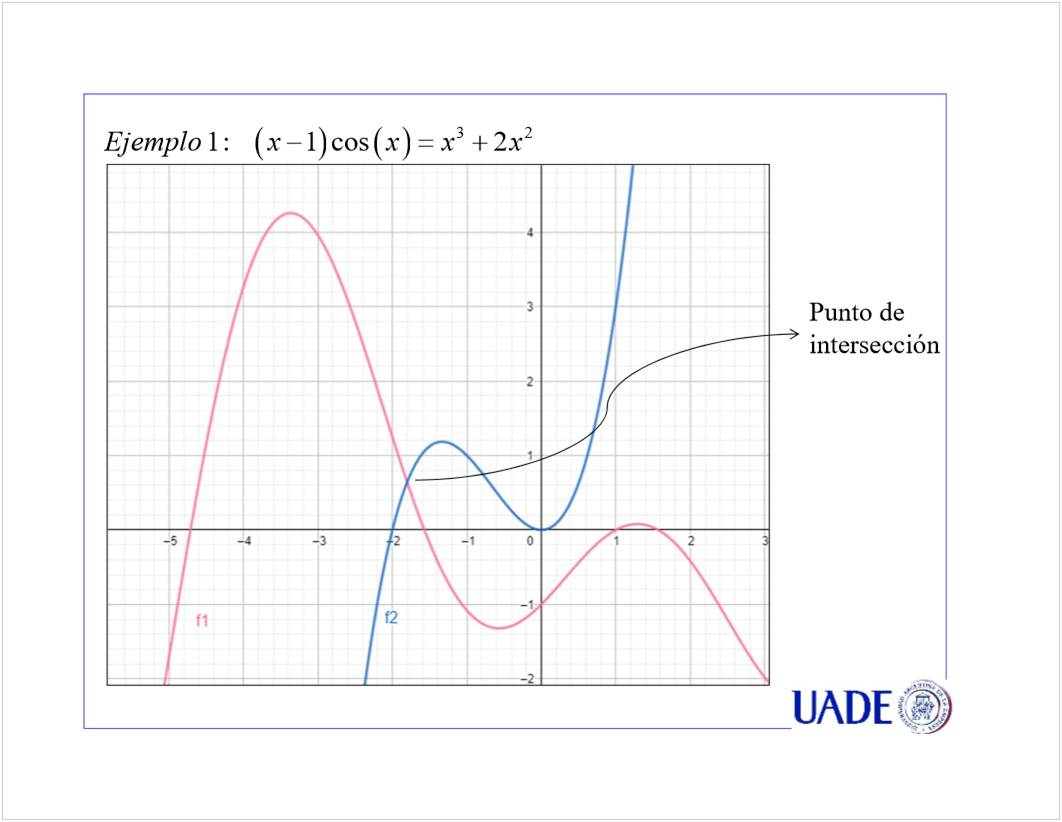
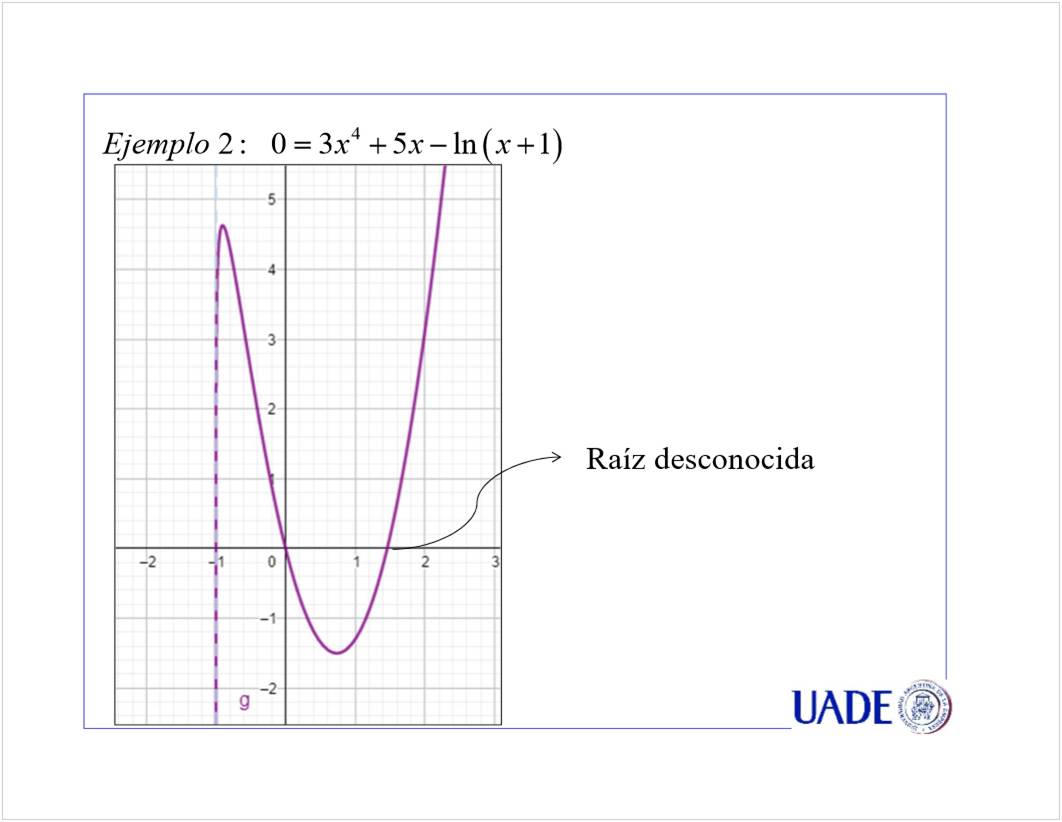
TPs

domingo, 9 de marzo de 2025

00:57

 

TP1

Wednesday, June 8, 2022

6:48 PM

 

<<CN TP 1 2021.pdf>>

 

Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings 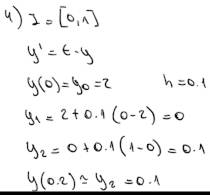Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings práctia 1 C"ulo b) Considerando k —1/2, —25% discretizar el problerna por el métodode en el intervalo Con paso h a elección. utilizando Octave, representar en un gráfico la solución exacta y la aproximada. En el intervalo I (O, II se define la ecuación diferencial de primer orden Calcular, mediante el método de un valor aproximado de sabiendo que VIO) 2 V considerando Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings

 

Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings

 

TP2

Tuesday, June 21, 2022

8:23 PM

 

<<CN TP 2 2021.pdf>>Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings 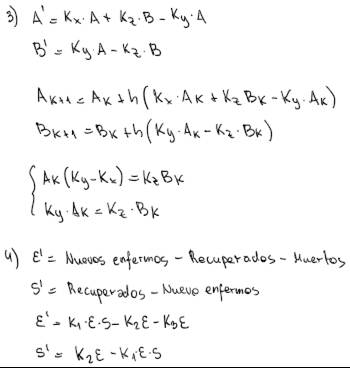Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings

 

 

Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings

 

TP3

Tuesday, June 21, 2022

8:22 PM

 

<<CN TP 3 2021.pdf>>Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings

 

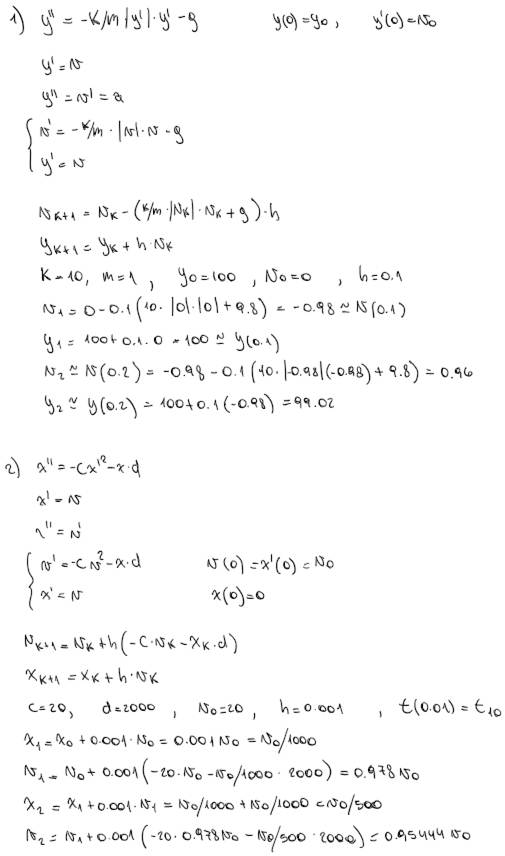
Entrega II

Wednesday, June 22, 2022

4:35 PM

 

<<Entrega II.pdf>>

 

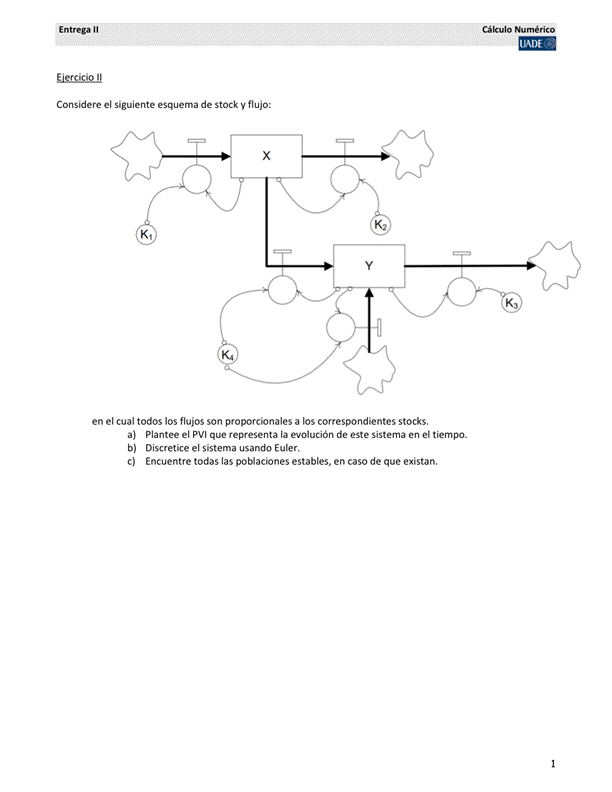
C"ulo Considere el siguiente esquema de Stock flujo: K, en el cual todos los flujos son proporcionales a los correspondientes stocks. a) plantee el que representa la evolución de Sistema enel tiempo. b) Discretice el sistema usando Euler, c) Encuentre todas las poblaciones estables, en caso de que existan. Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings

 

Entrega III

Wednesday, June 22, 2022

5:03 PM

<<Entrega III.pdf>>Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings

 

 

Exámen

domingo, 9 de marzo de 2025

00:58

 

Para el parcial

Wednesday, June 22, 2022

7:34 PM

 

 

Rk no entra

 

Una de Euler

Una de stock y flujo

Una No lineal cambio de variable

Una teorica de ultimo tema

 

Parcial Simulacro

Wednesday, June 22, 2022

7:40 PM

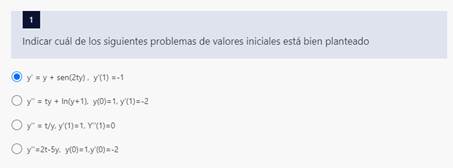
Indicar cuál de los siguientes problemas de valores iniciales está bien planteado —y + sen(2ty), y'(l) ¯ ty + In(y+l), y(0) =2t-5y,

 

La siguiente expresión se obtuvo luego de aplicar el método de Euler a cierta ecuación diferencial. ¿Cuál es dicha ecuación? Yk+l = ' -tA3-4yt -tA3 + 4ty=o -tA3 + 4t=o Yk + tk? ¯ 4Yktk)

 

Si al aplicar el método de Euler se obtiene y_k ¿Es cierto que las iteraciones siguientes son odas iguales a cero? Justificar

 

Explicar cuáles son las condiciones que tiene que cumplir una función f para que el método de Bolzano encuentre, aproximadamente, un cero de f en un intervalo [a, b]

Para que se pueda utilizar el metodo de Bolzano en el intervalo [a,b], una funcion debe ser continua en (a,b) y debe tener al menos dos puntos de signo opuestos.

 

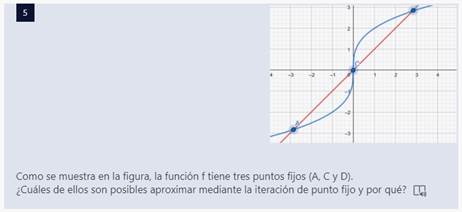
Como se muestra en la figura, la función f tiene tres puntos fijos (A, C y D). ¿Cuáles de ellos son posibles aproximar mediante la iteración de punto fijo y por qué?

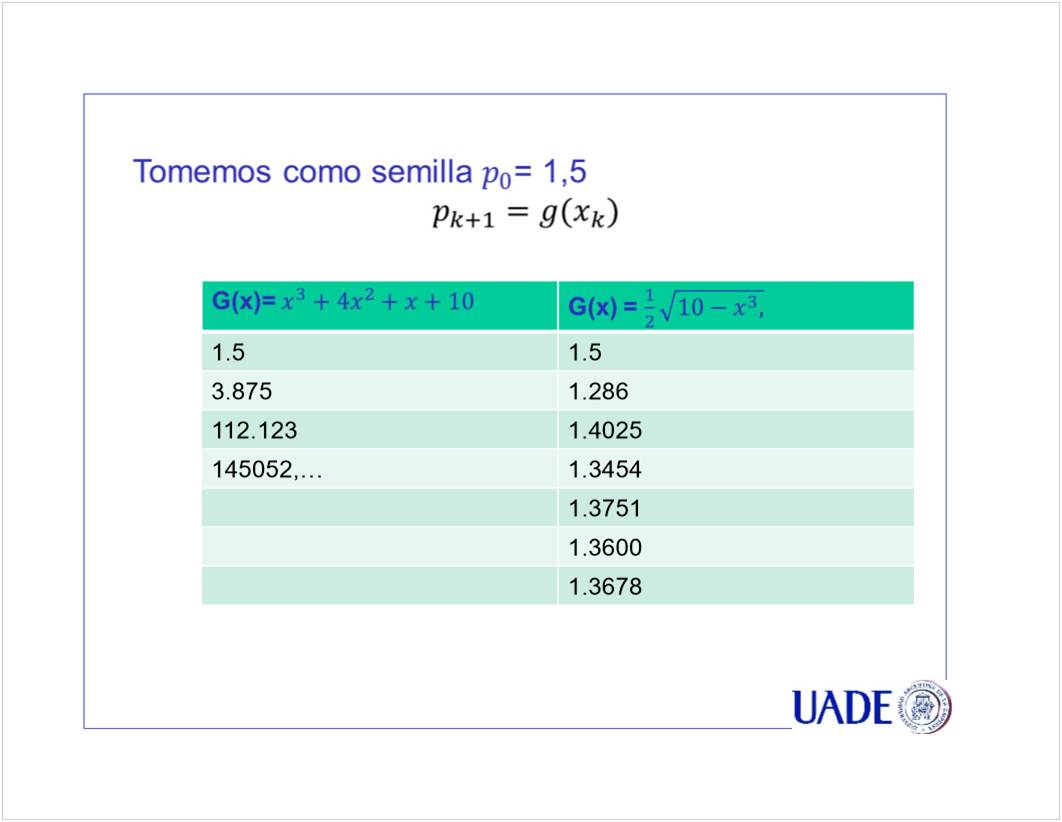
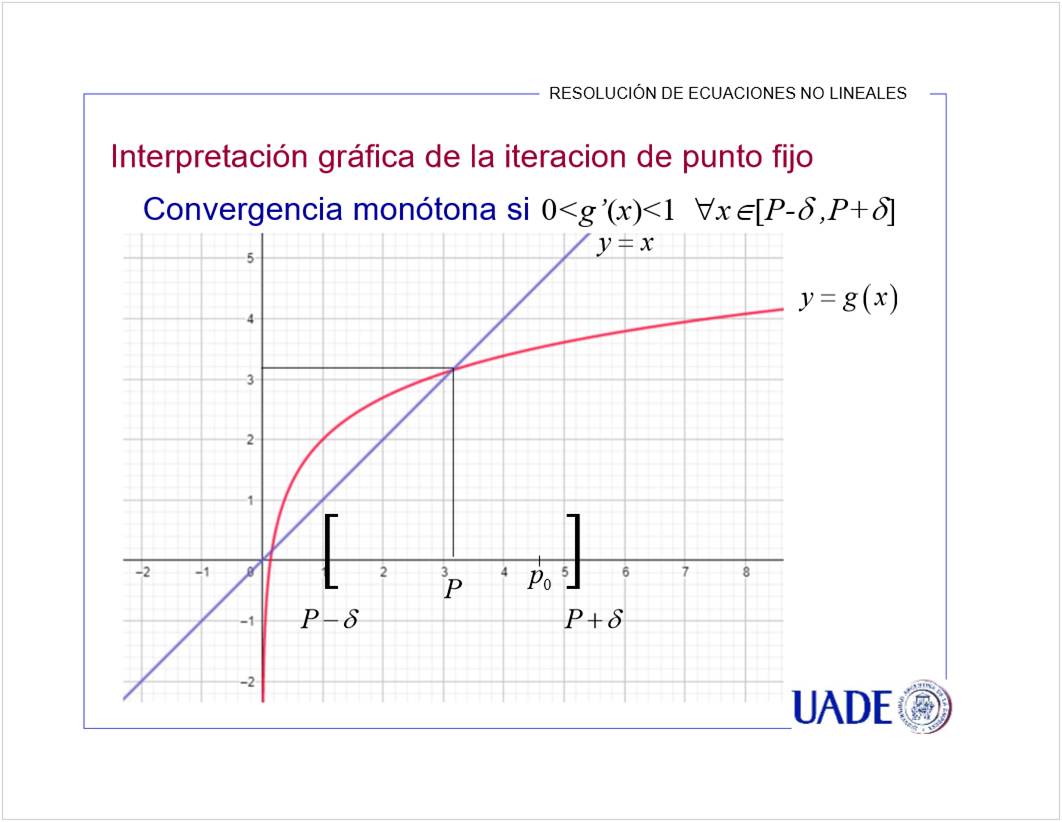
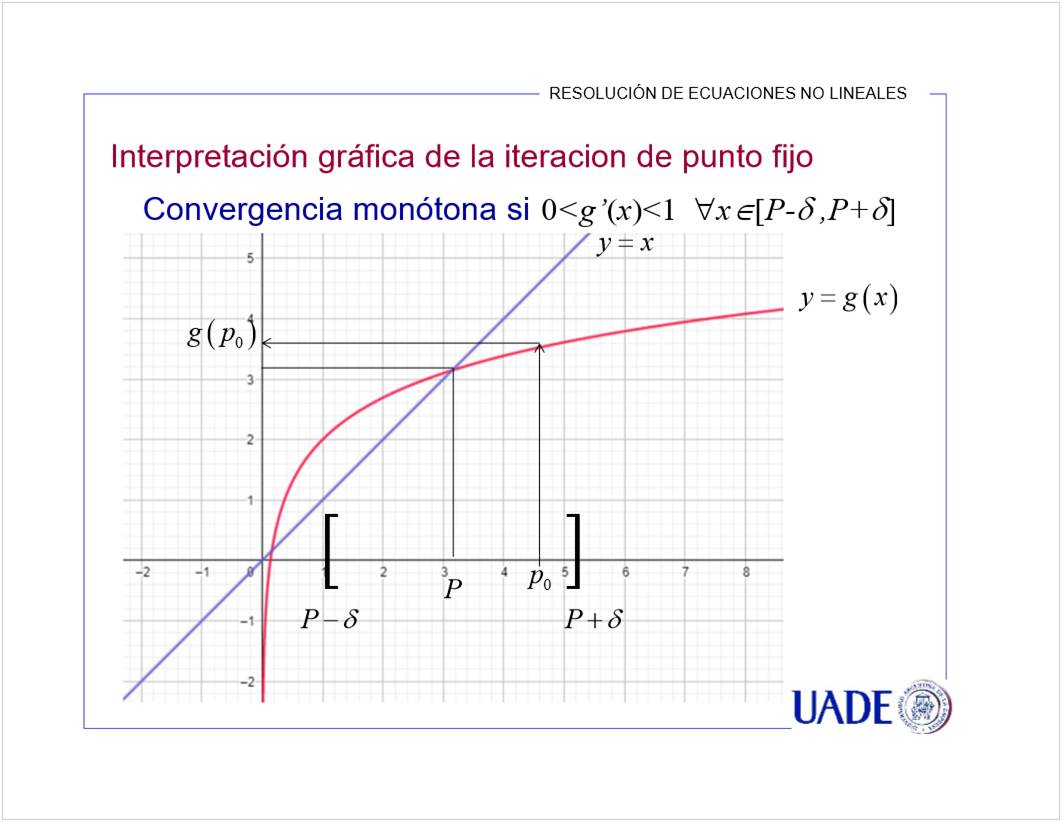
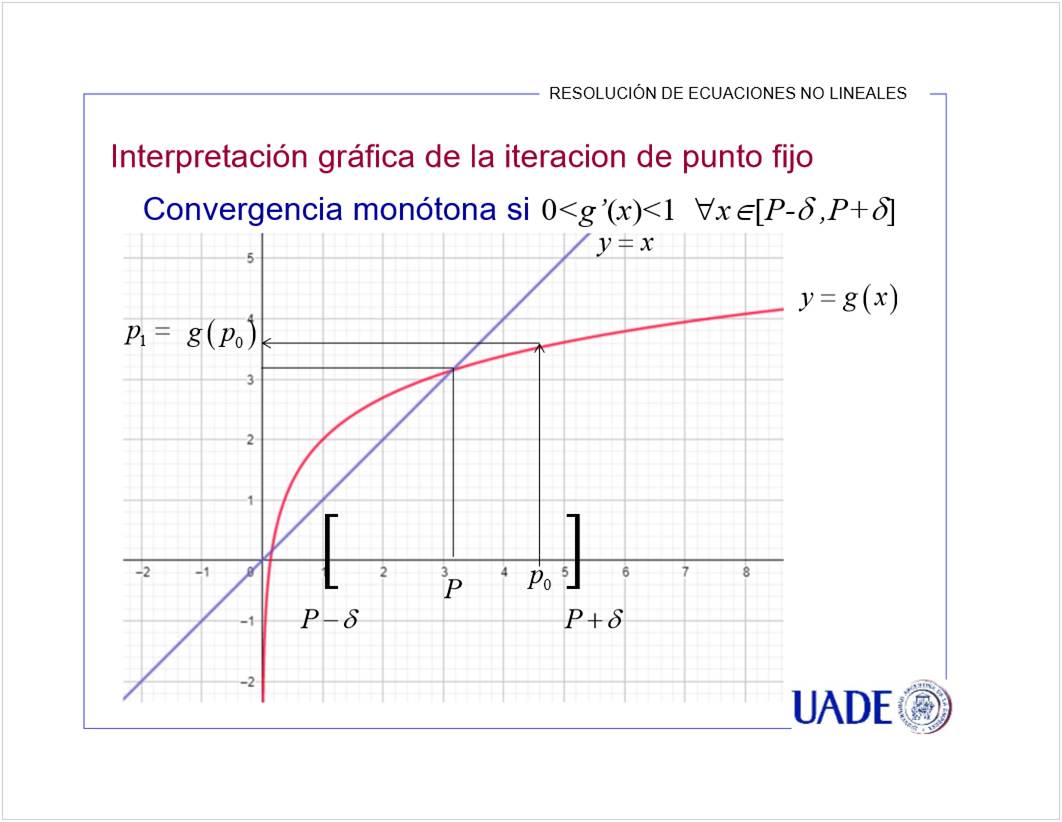
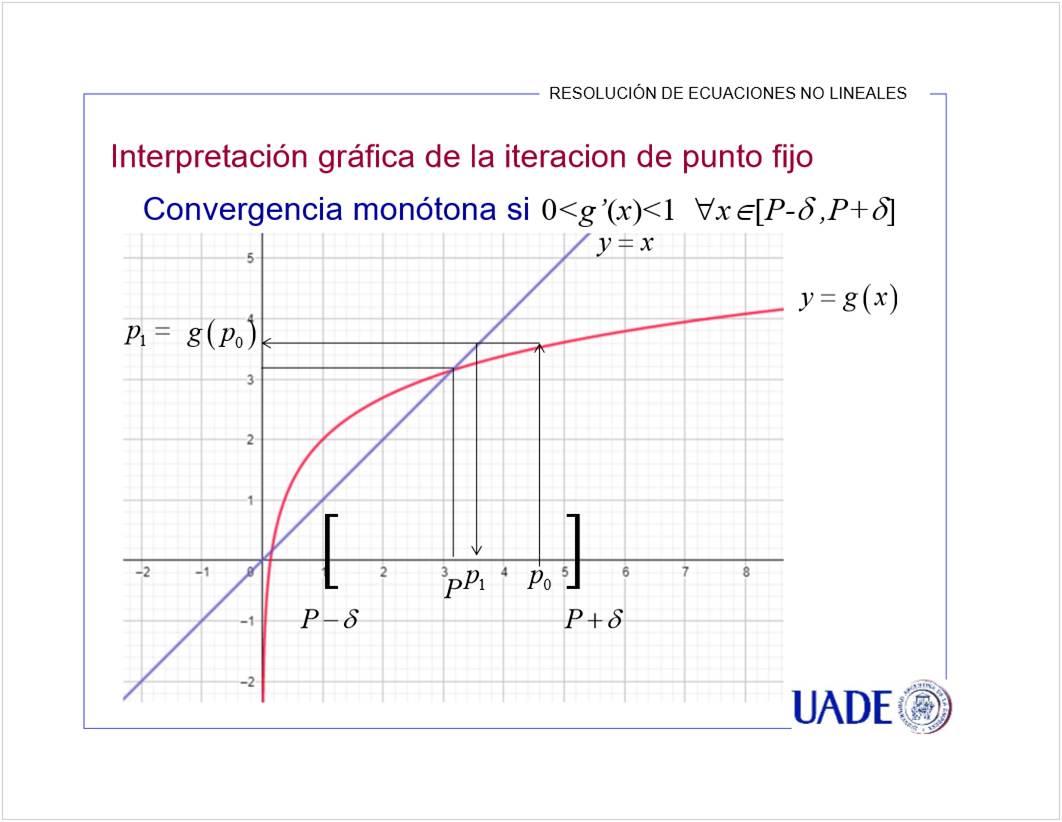
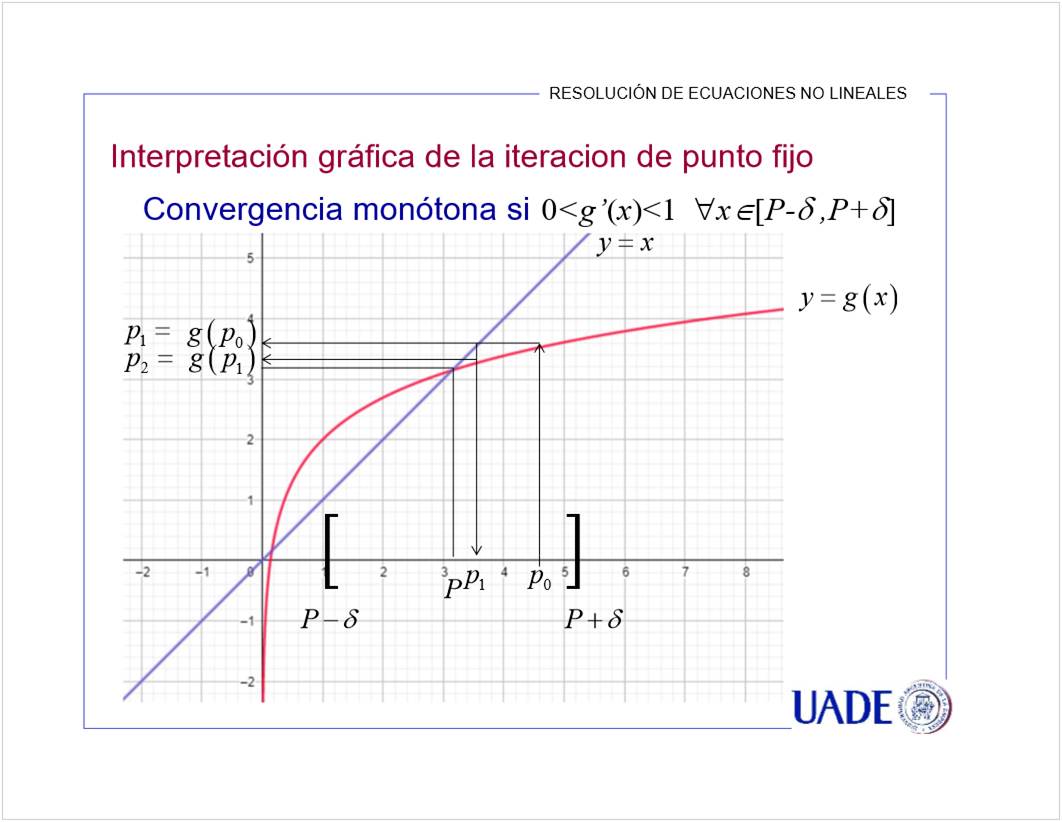
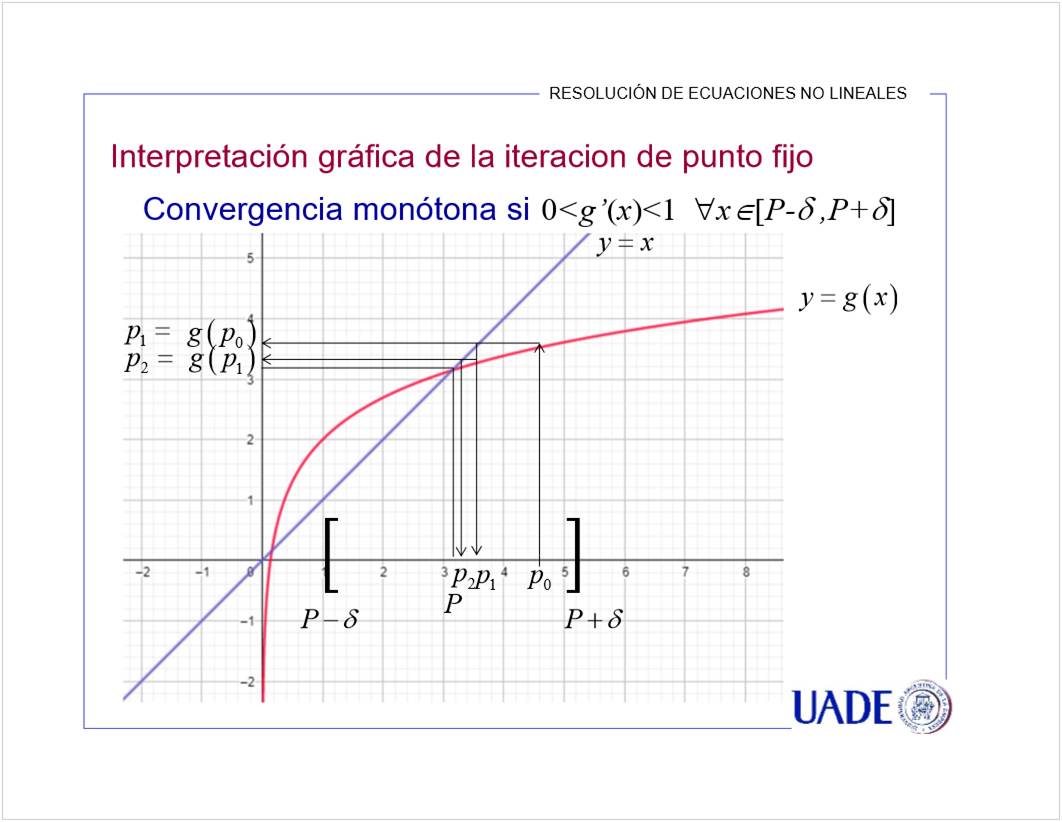
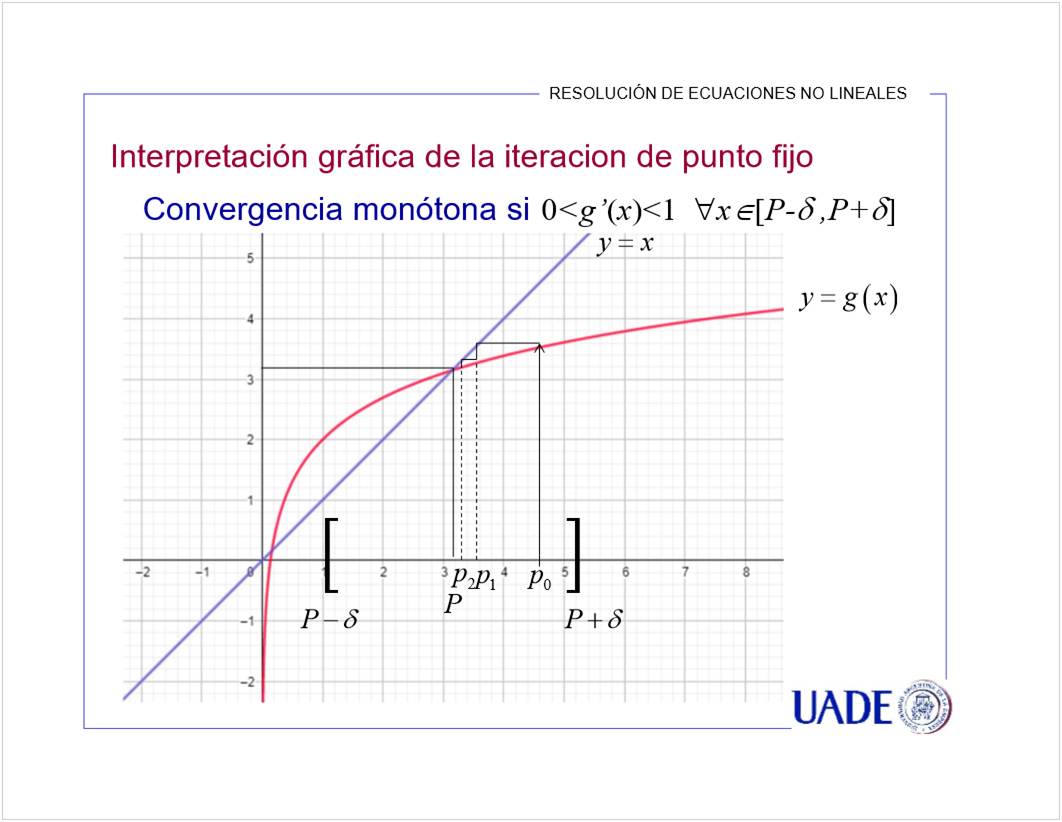
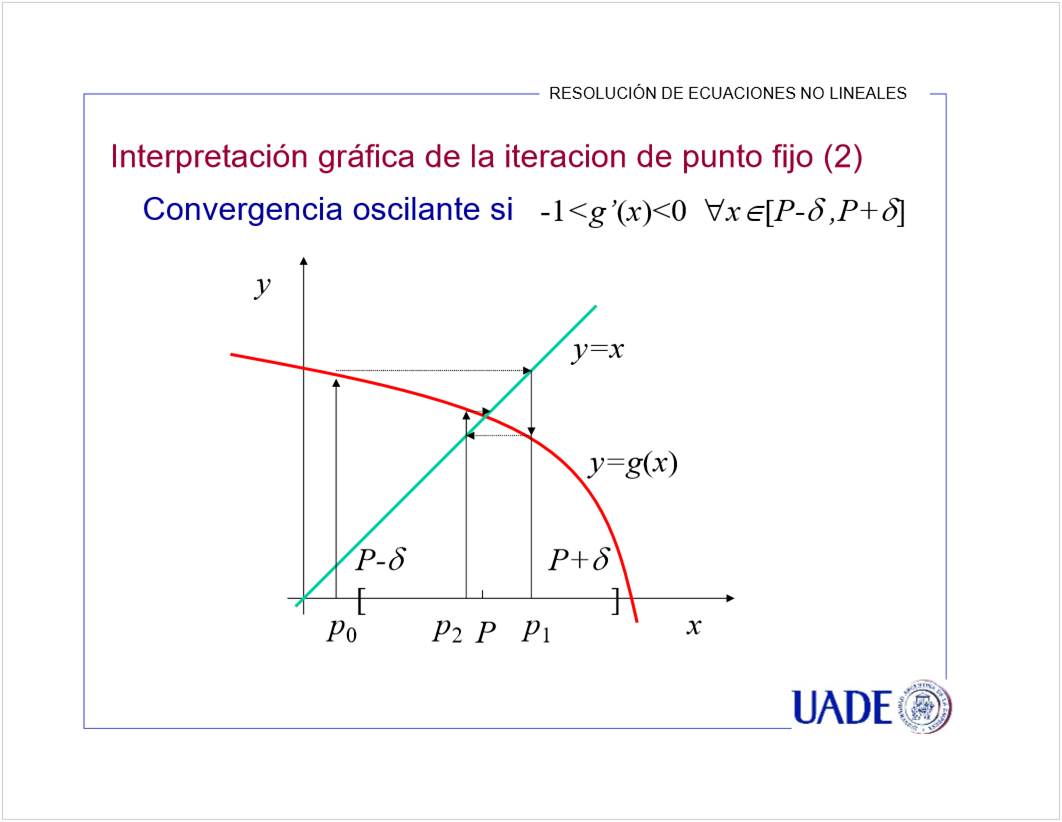
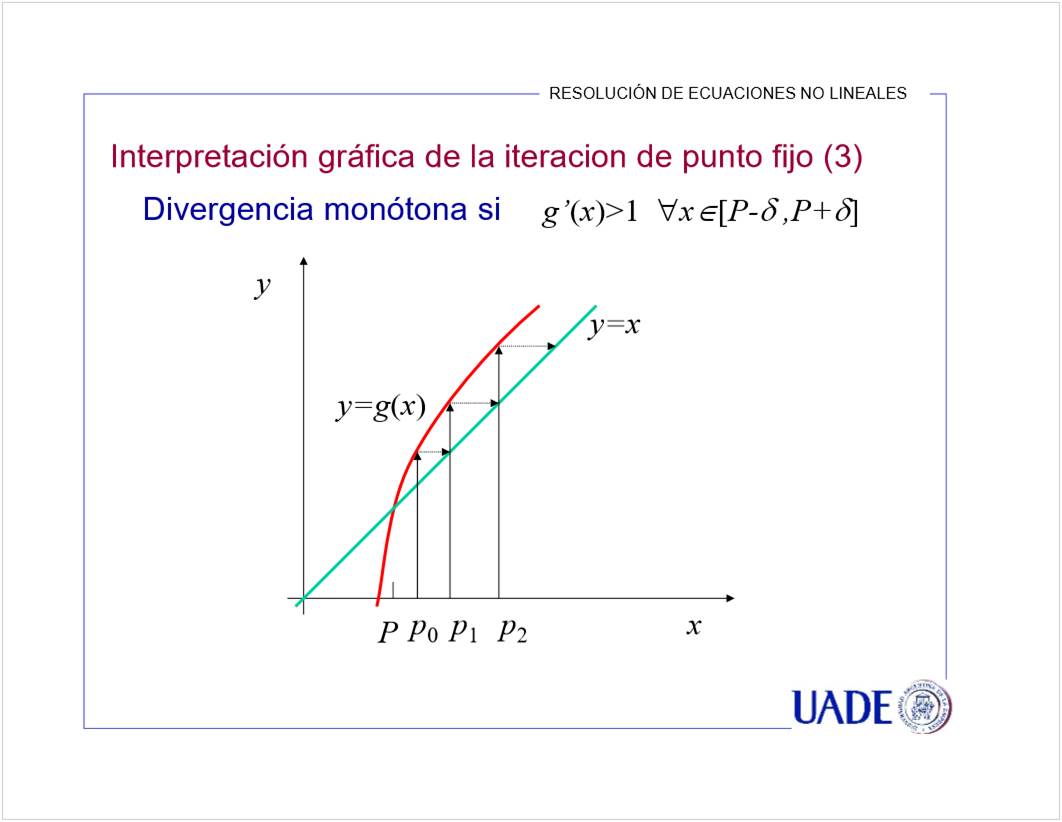
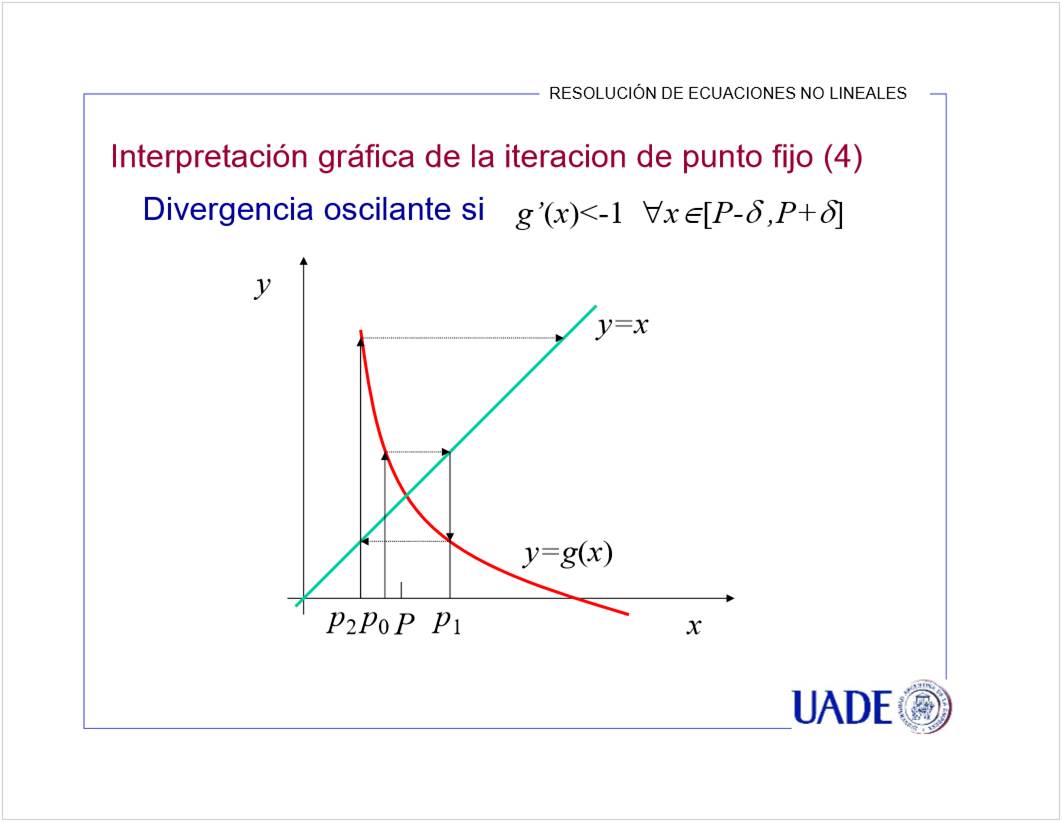
Se puede en A y D porque su derivada es menor a 1. El crecimiento es lento, entonces se estabiliza la aproximacion.

 

2t3 _ Dada la siguiente ecuación diferencial de segundo orden definida en 2]se pide: a) Plantearla como un sistema de EDO de orden uno. b) Discretizar mediante el método de Euler c)Calcular un valor aproximado de considerando h (Non-enonymous question@) *

 

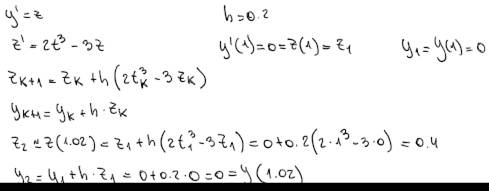
Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings

 

 

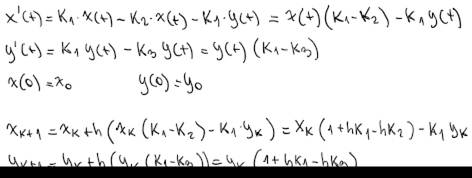
Dado el siguiente diagrama de stock y flujo con X(O) =xO, a)Plantear el sistema de ecuaciones diferenciales representado en el diagrama b) Discretizar mediante el método de Euler (Non-enonymous question@) x Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings

 

Resumen Parcial

Tuesday, June 28, 2022

4:58 PM

 

Euler

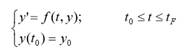
y(to) = Yo

 

Yk+l k-1.2, „„M ı y(to) Yo

 

Sistema de ecuaciones

con { x(to) y(to) en el intervalo [to,tF]

 

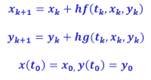
Yk+l = Yk + x(to) = Xo, y (to) = Yo

 

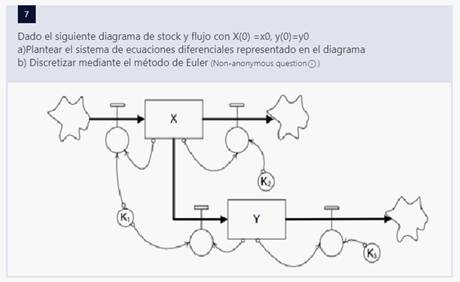
Diagramas de stock y flujo

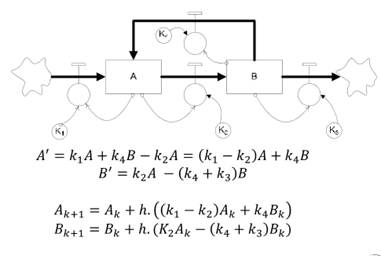
.4' = k1A + - k2A = (k1 -К2)А + В' = ,k2A - (k4 + Кз)в ,4k+1 = Ак + h. ((k1 - К2)Ак + КИК) (К4 Кз)Вк)

 

Orden Superior

Yn-l y' en el intervalo [to,tF] • • Yn—l ) Yn-l ) Yo Yl (to) Yo y(to) = Yo en to

 

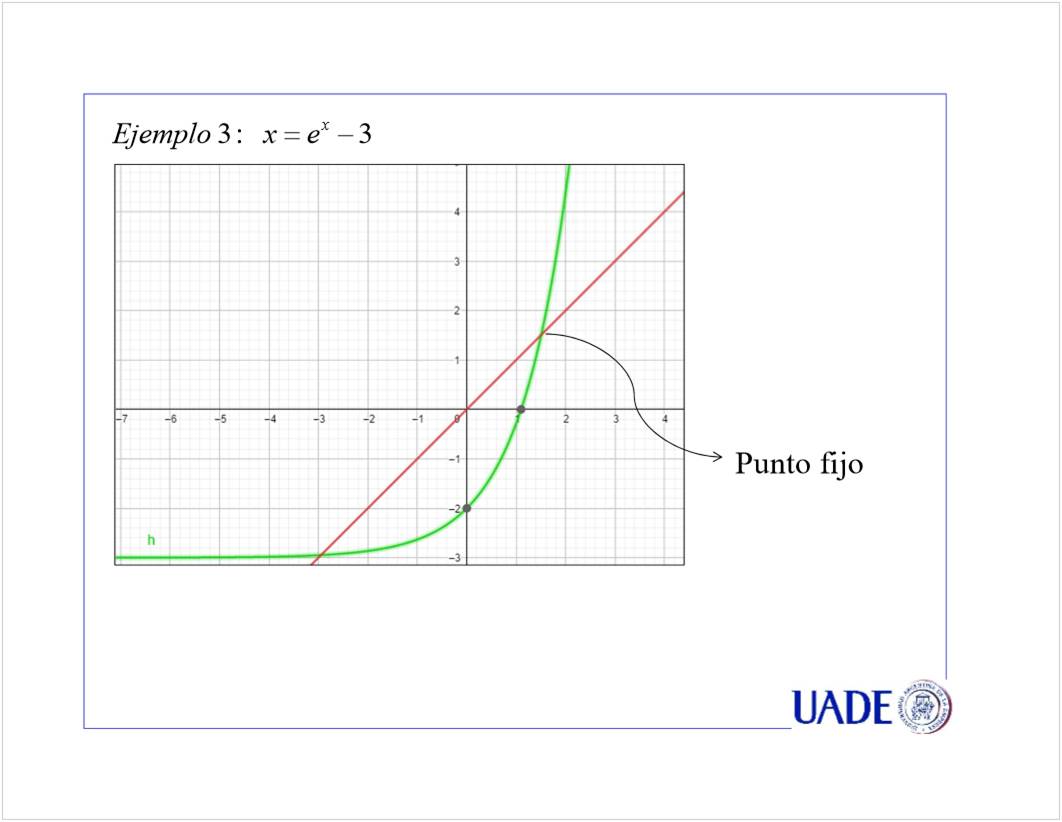
No lineal

 

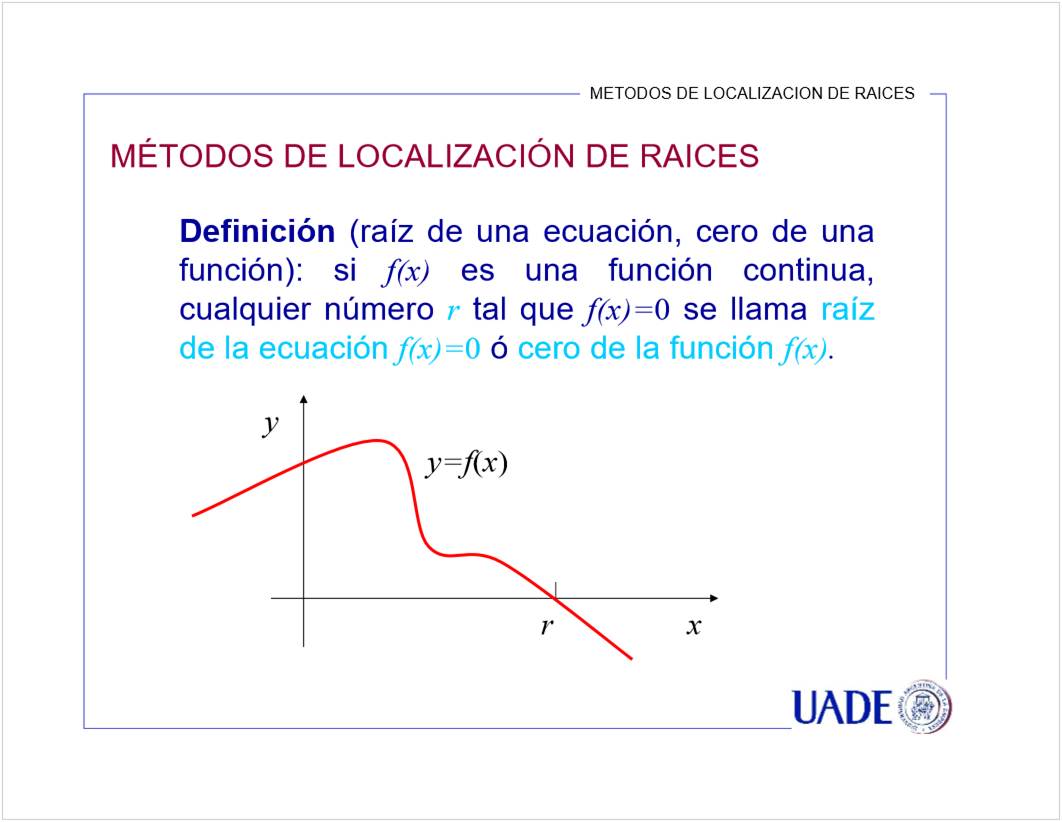
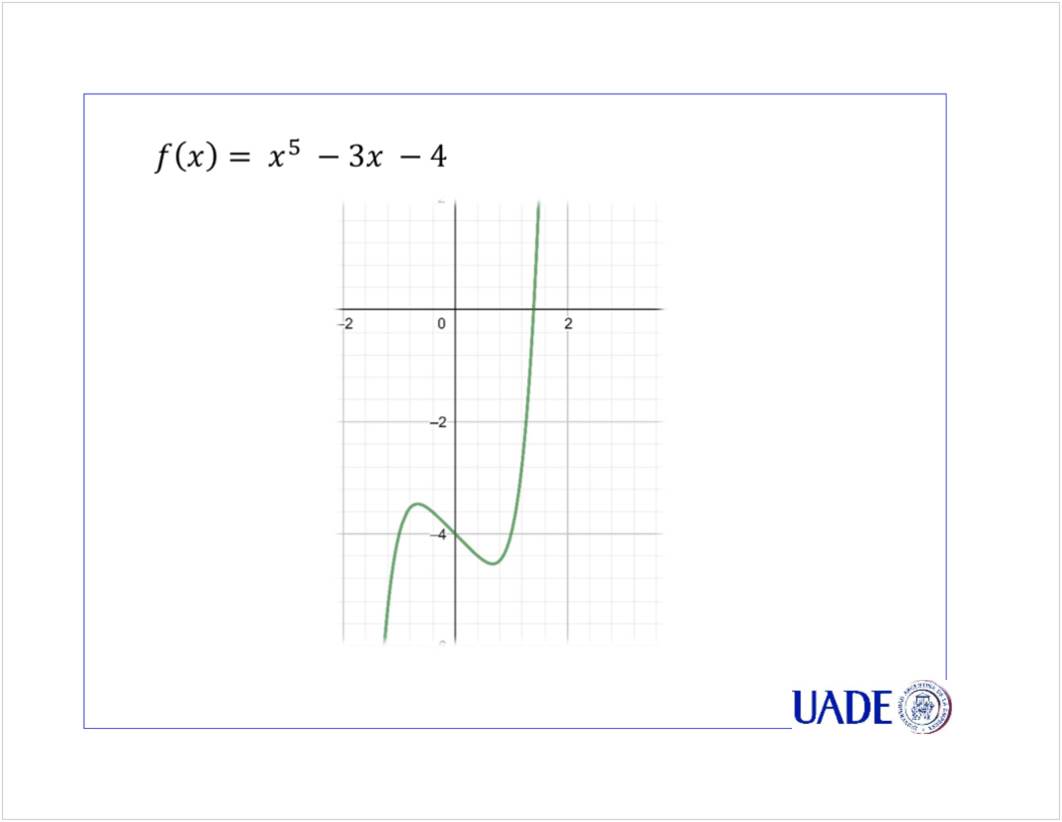
PROBLEMAS A RESOLVER Nos referiremos a tres tipos de problemas: Se trata de 'Hallar x tales que _ 2. [puntos de intersección] [localización de raíces] [puntos fijos] _ 0 g(x)"

 

Cualquiera de los 3 problemas se puede convertir en uno de los otros

 

Teorema de Bolzano Sea f una función continua en un intervalo [a, b] tal que f(a)f(b)< O. Entonces existe c e (a, b) tal quef(c )

 

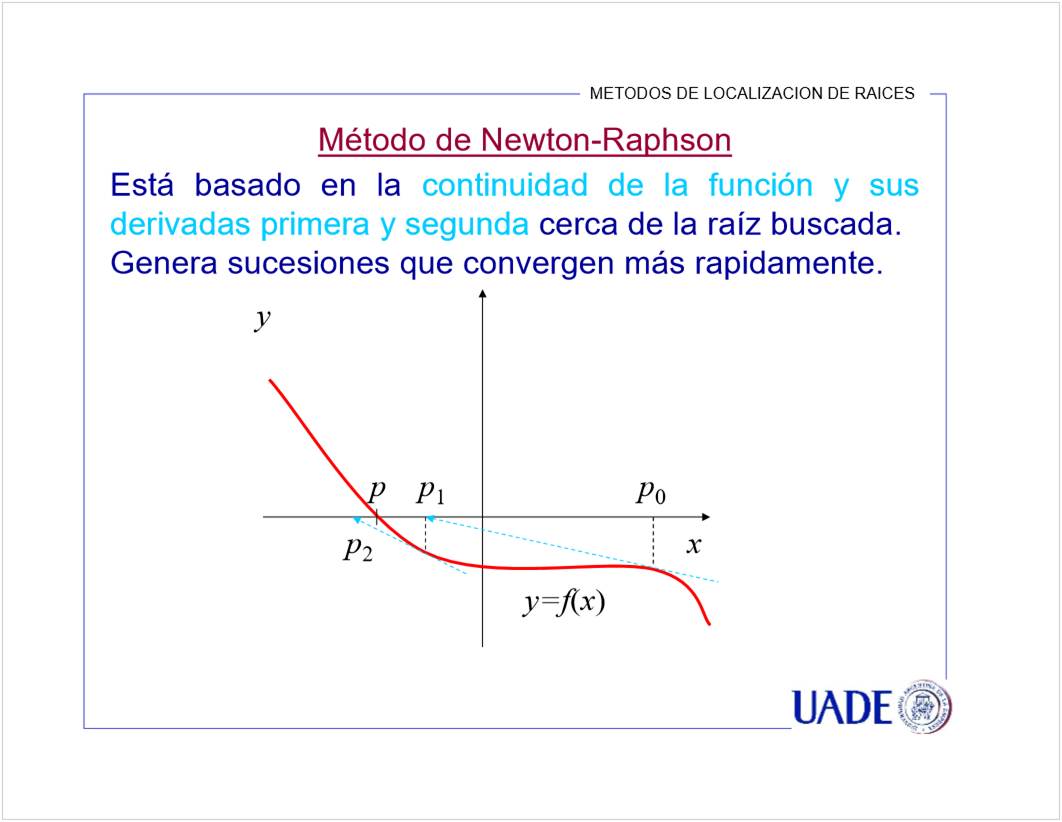
Teorema de Newton-Ra hson Supongamos que Sp [a, b] tal que f (p) 0 y que además f y f'(p) Entonces existe una distancia > O tal que la sucesión f(Pk-l ) g(Pk-1) converge generada por Pk = Pk-l ¯ f' (Pk-l) ap cualquiera sea la semilla po e Observación: La función se llama función de iteración de ewton- ap son.

 

Puntos fiios Definición: Un punto fijo de una función g(x) es un número real P tal que P=g(P). Definición: La iteración para . llama iteración de punto fijo se Teorema: Sean la función continua gy una sucesión generada por iteración de punto fijo. Si limk.Ak=P, entonces P es un punto fijo de g(x).